You can
put this solution on YOUR website! .
P(A | B) actually means and is the same as P(A ∩ B)/P(B).
Therefore, the given P(A | B) = 0.3855 means that P(A ∩ B)/P(B) = 0.385.
Multiplying both sides of the last equality by P(B), you get
P(A ∩ B) = 0.385*P(B) = 0.385*0.35 = 0.13475.
To find P(A U B), use the general formula
P(A U B) = P(A) + P(B) - P(A ∩ B) = 0.39 + 0.35 - 0.13475 = 0.60525.
Last step, P(B|A) = P(B ∩ A) / P(A) = P(A ∩ B) / P(A) = 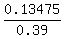 = 0.345513.
= 0.345513.
Solved. I answered all questions.
-------------------
If you want to see many similar solved problems and learn more on conditional probability, look into the lessons
- Conditional probability problems
- More conditional probability problems
in this site.