SOLUTION: Two numbers are randomly selected (with replacements) from the first 12 positive integers. What is the probability that the sum of these two numbers is 10?

Click here to see ALL problems on Probability-and-statistics

Question 1150462: Two numbers are randomly selected (with replacements) from the first 12 positive integers. What is the probability that the sum of these two numbers is 10?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13198) (Show Source):
You can put this solution on YOUR website!

Answer deleted; I overlooked the "with replacements" in the statement of the problem.

Answer by ikleyn(52777) (Show Source):
You can put this solution on YOUR website!
.

The number of all possible outcomes is 12*12 = 144. It is the number of all pairs (a,b) with integers "a" and "b" from 1 to 12 inclusive. The favorable pairs are (1,9), (2,8), (3,7), (4,6), (5,5), (6,4), (7,3), (8,2) and (9,1). The number of favorable pairs is 9. The probability under the question is P = 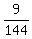= . ANSWER