.
A certain virus infects one in every 500 people.
A test used to detect the virus in a person is positive 90% of the time if the person has the virus
and 10% of the time if the person does not have the virus.
Let A be the event "the person is infected" and B be the event "the person tests positive."
(a) Find the probability that a person has the virus given that he or she is tested positive.
(b) Find the probability that a person does not have the virus given that he or she is tested negative.
Solution
(a) To make the solution easier, let assume that we have a population of 100,000 persons in the city.
According to the input data, 
of them, i.e. 
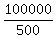= 200 are infected.
Of this 200 people, 90%, i.e. 0.9*200 = 180 are test positive.
The problem asks in (a), what is the ratio of the number of those who are test positives AND have the virus
to the number of infected.
It is obvious that this ratio is P =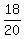 
= 0.9 = 90%. ANSWER
In the compact form, a formula for the probability (a) is P = 
= 0.9.
(b) The probability under question (b) is the ratio of the number of those who do not have a virus AND are tested negative
to the number of those who do not have the virus.
The number of those who do not have the virus is 100000 - 0.002*100000 = 100000 - 200 = 99800.
Of them, the number of those who are tested negative is (1-0.1)*99800 = 0.9*99800 = 89820.
With these numbers, the probability (b) is
P = 
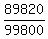= 0.9. ANSWER
In the compact form, a formula for probability (b) is P =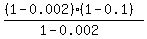 
= 0.9.
Solved.
