Question 1145327: 2.An insurance company has information that 93% of its auto policy holders carry collision coverage or unsecured motorist coverage on their policies. Eighty percent of the policy holders carry collision coverage, and 60% have unsecured motorist coverage.
i.What percentage of these policy holders carry both collision and unsecured motorist coverage?
ii.What percentage of these policy holders carry collision but not unsecured motorist coverage?
Found 2 solutions by VFBundy, ikleyn:
Answer by VFBundy(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! i.What percentage of these policy holders carry both collision and unsecured motorist coverage?
47%
ii.What percentage of these policy holders carry collision but not unsecured motorist coverage?
33%

Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem uses VERY long (EXTREMELY long) descriptive names of the objects.
They make it intently, to confuse you.
So, to simplify the solution, you need to make two preliminary things:
- first is to give short names to these objects (subjects): call them "category A" and "category B".
- then re-formulate the problem using these short names.
Now the problem short formulation is THIS :
there are two sets A and B. Together, they comprise 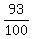 of the entire universal set.
Category A is of the entire universal set.
Category A is 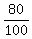 of the entire set; category B is of the entire set; category B is  of the universal set.
Questions: a) how much is the intersection (A intersection B) in terms of the universal set ?, and
b) how much is the difference of sets A \ (A intersection B) in terms of universal set ?
In the elementary set theory, there is a universal formula
m(A U B) = m(A) + m(B) - m(A intersection B). (1)
Here, "universal" means that it is equally applicable to any two subsets A and B of the "parent" set and that "m" is any reasonable
measure of subsets: their size relative to the "parent" size; or simply the number of elements in subsets; or probability;
or percentage to the "parent", as it is in this case.
In your given case, this basic equation (1) takes the form
93 = 80 + 60 - m(A intersection B). (2)
You need to find m(A intersection B), (it is your first question), and from equation (2) you find it MOMENTARILY :
m(A intersection B) = 80 + 60 - 93 = 140 - 93 = 47.
The second question is to find m(A \ (A intersection B)).
Obviously, it is m(A) - m(A intersection B) = 80 - 47 = 33.
Thus the answers are 47% to the first question, and 33% to the second. of the universal set.
Questions: a) how much is the intersection (A intersection B) in terms of the universal set ?, and
b) how much is the difference of sets A \ (A intersection B) in terms of universal set ?
In the elementary set theory, there is a universal formula
m(A U B) = m(A) + m(B) - m(A intersection B). (1)
Here, "universal" means that it is equally applicable to any two subsets A and B of the "parent" set and that "m" is any reasonable
measure of subsets: their size relative to the "parent" size; or simply the number of elements in subsets; or probability;
or percentage to the "parent", as it is in this case.
In your given case, this basic equation (1) takes the form
93 = 80 + 60 - m(A intersection B). (2)
You need to find m(A intersection B), (it is your first question), and from equation (2) you find it MOMENTARILY :
m(A intersection B) = 80 + 60 - 93 = 140 - 93 = 47.
The second question is to find m(A \ (A intersection B)).
Obviously, it is m(A) - m(A intersection B) = 80 - 47 = 33.
Thus the answers are 47% to the first question, and 33% to the second.
Solved, explained, completed, answered.
-------------------
For your education, look into the lesson
- Counting elements in sub-sets of a given finite set
in this site. After reading this lesson, you will understand formula (1) much better.
/\/\/\/\/\/\/
To the tutor @EFBundy :
I like your style working at this forum.
|
|
|