SOLUTION: A company owns a fleet of 20 cars, each having either manual or automatic transmission and either 2 or 4 doors. It is reported that 13 cars are 2-door models and, of these, 12 have

(1)  Consider first statement of the problem:

          Of the total fleet of 20 cars, 13 cars are 2-doors.  


     From this statement,  20-13 = 7 cars are 4-doors.



(2)  Consider the second and the third statements:

         of the 13 2-doors cars, 12 have automatic transmission (AT).

         There are only 4 cars with manual transmission (MT).


     From these two statements, one can make the following conclusions:


         - Of the 13 2-doors cars, 1 has manual transmission;

         - of the  7 4-doors cars, 3 have manual transmission and 4 have automatic transmission.


Let us ORGANISE this information.


    There are  13 2-doors cars; of them, 12 have AT and 1 have MT.

                7 4-doors cars; of them,  4 have AT and 3 have MT.



Now I am in the position to answer problem's questions.

    (A)  P = .                  ANSWER

    (B)  P =  =  = .    ANSWER

The key in solving this problem is to organize and to present the information in a compact and clear logical form.


To get it, you need to extract / (to deduce) all logical consequences from the given info.


Surely, it is assumed, that you firmly know this formula for the conditional probability


    P( M | N ) = ,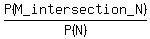


where M and N are subsets of the universal set.