Question 1141988: In a study of the accuracy of fast food drive-through orders, Restaurant A had 284 accurate orders and 63 that were not accurate.
a. Construct a 95% confidence interval estimate of the percentage of orders that are not accurate.
b. Compare the results from part (a) to this 95% confidence interval for the percentage of orders that are not accurate at Restaurant B: 0.156less thanpless than0.245. What do you conclude?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part A
At 95% confidence, the critical z value is roughly z = 1.960
To find this value, I used this table.
More specifically, I looked at the row starting with Z (near the very bottom of the table) and looked above the 95% confidence level to find the value 1.960

Use of the invNorm function on your TI83 or TI84 calculator will yield the same approximate results (though more accurately of course).
---------------
Use that z critical value, along with  to compute the margin of error (MOE) to compute the margin of error (MOE)
}{n}})
}{284}})

---------------
Now compute the lower boundary (L) of the confidence interval
L = lower boundary
L = phat - MOE
L = 0.22183 - 0.04832
L = 0.17351
L = 0.174
Do a similar computation for the upper boundary (U)
U = upper boundary
U = phat + MOE
U = 0.22183 + 0.04832
U = 0.27015
U = 0.270
---------------
---------------
The approximate confidence interval is (L, U) = (0.174, 0.270) meaning the percentage of inaccurate orders ranges from 17.4% to 27.0% (and we are 95% confident of this claim)
The notation (0.174, 0.270) is the same as writing 0.174 < p < 0.270 because p is the parameter we're trying to estimate.
===================================================================================
Part B
In part A, we found the confidence interval found to be roughly 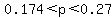 for restaurant A. for restaurant A.
In part B, we're told that restaurant B has a confidence interval of 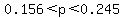
Let's draw out a number line and plot the two confidence intervals. I'm going to stack them so that we can tell them apart, and the diagram below shows an overlapping region starting from point A and ending at point D.

The blue interval is for restaurant A. The red interval is for restaurant B.
There is overlap. For example, p = 0.220 is possible for both intervals, which means that both restaurants could have a 22.0% inaccuracy rate. If there was no overlap of the intervals, then it would be impossible for p to be the same value for both restaurants. So again, we could conclude that the restaurants could have the same inaccurate order rate due to the overlap. Though of course this isn't fully guaranteed.
side note: The endpoints A,B,C,D in the diagram are shown as open holes. This is to visually say "do not include this value as part of the confidence interval". This is due to a compound inequality like 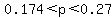 having "less than" signs rather than "less than or equal to" signs. having "less than" signs rather than "less than or equal to" signs.
|
|
|