Question 1137840: Suppose that an investor intends to buy stock in two companies. He has narrowed his
interest to 5 stocks -- 3 industrials ( I1 , I2 , I3 ) and 2 utilities ( U1 , U2 ). Suppose the
investor chooses 2 of these 5 stocks at random. (Note: They must be different stocks!
For example, I1 and I2 are different stocks as are I1 and U1.)
(a) Display the sample space (S) of equally likely outcomes. [Note that the order in
which the two stocks are chosen is not important. So if ( I2, U1 ) are chosen, that is
the same as selecting ( U1, I2 ) ].
(b) Let event A = the investor chooses 2 industrial stocks. Find P(A).
Found 2 solutions by jim_thompson5910, ikleyn:
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website!
Part A
Make a table that looks something like this
The stuff in red along the rows is the first stock picked while the stuff in blue along the columns is the second stock picked.
Each cell in the form (x,y) is a result of picking one of each color.
Eg: row 2, column 4 has (I2, U1) in it from red I2 along the left hand side and the blue U1 up top. You can think of it as a game of battleship in terms of how you locate a ship you want to target.
Mark out the main diagonal. I'm doing so in yellow highlighter
This main diagonal is where you pick the same stock twice. This isn't possible, so we will ignore this diagonal and anything below it (the stuff below the diagonal is a symmetric copy of the stuff above the diagonal). The cells we ignore can be blotted out like so
The stuff that isn't covered up forms the sample space
S = sample space
S = set of all possible ways to pick 2 stocks
S = {(I1, I2), (I1, I3), (I1, U1), (I1, U2),
(I2, I3), (I2, U1), (I2, U2),
(I3, U1), (I3, U2),
(U1, U2) }
This formatting mimics the pattern in how the remaining ordered pairs show up in the table. Otherwise things could get a bit cluttered. The curly braces tell the reader "this is a set".
Extra info:
There are 4 items in row 1
There are 3 items in row 2
There are 2 items in row 3
There is 1 item in row 4
In total, there are 4+3+2+1 = 10 items in the sample space.
------------------------------------------------------------------------------------------
Part B
A = event that investor picks two industrial stocks
A = set of all pairs (x,y) such that x and y are picked from {I1,I2,I3}
A = { (I1, I2), (I1, I3), (I2, I3) }
We can see this by highlighting these cells below
There are 3 ways to get what we want out of 10 items total (sample space size)
The answer as a fraction is 3/10
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
Shortly saying,
(a) the sample space is the space of all subsets of the given set, consisting of 2 elements, or, in other words,
The sample space is the set of all pairs (X,Y), where X and Y are different names from the given list of companies.
In combinatorics, such type of sets is calling "combinations of 5 names of the companies taken 2 at a time".
The number of elements in the sample space is 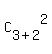 =  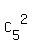=  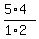= 10.
(b) Investor can select 2 of the 3 industrial stokes by  =  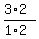=  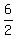= 3 ways.
So the probability of event A under question (B) is P(A) =  = 0.3.
Solved.
------------------
On Combinations, see introductory lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
/\/\/\/\/\/\/\/
This my post is not to argue with the solution by Jim Thompson, which is absolutely correct.
It is to get you familiar with the terminology and key conceptions of Combinatorics, that are adjacent to this Probability problem.
|
|
|
