SOLUTION: Suppose a pair of fair dice is rolled once. Find the probability of rolling: A sum of 8 or greater given that one of the dice is a 4

Algebra ->  Probability-and-statistics -> SOLUTION: Suppose a pair of fair dice is rolled once. Find the probability of rolling: A sum of 8 or greater given that one of the dice is a 4       Log On


   

Question 1137809: Suppose a pair of fair dice is rolled once. Find the probability of rolling:
A sum of 8 or greater given that one of the dice is a 4


Found 2 solutions by jim_thompson5910, ikleyn:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

One of the dice is 4, so the other dice must show one of these values
{4, 5, 6}
in order to have the sum be 8 or greater

4+4 = 8
4+5 = 9
4+6 = 10
You can see that the blue die is held fixed to be that given 4, while the red die is allowed to vary as long as the two dice values add to something 8 or larger.

There are 6 ways to roll a die, and 3 of which are outcomes we want {4,5,6}. So the probability of having the red die land on those three values is 3/6 = 1/2 assuming each face is equally likely to land on.

Therefore, the final answer is 1/2

Edit: I may have made an error, so the tutor @ikleyn is probably correct. My apologies if 1/2 isn't the answer.

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

The full space of events is the set of all pairs  (i,j), where i and j are integer numbers from 1 to 6, inclusively.

This space consists of  6*6 = 36 elements.


Of them, the outcomes where the sum is 8 or greater, are


    sum  8 :  (2,6), (3,5), (4,4), (5,3), (6,2)     In all, 5 pairs.

    sum  9 :  (3,6), (4,5), (5,4), (6,3)            In all, 4 pairs.

    sum 10 :  (4,6), (5,5), (6,4)                   In all, 3 pairs.

    sum 11 :  (5,6), (6,5)                          In all, 2 pairs.

    sum 12 :  (6,6)                                 Only    1 pair.


Thus the number of events where the sum is 8 or greater is  5 + 4 + 3 + 2 + 1 = 15.


Of them, the number of pairs, where at least one component is 4, is equal to 5 : (4,4), (4,5), (5,4), (4,6) and (6,4).


Starting from this point, you can find the answer to the problem's question in two ways.


1-st way.   "Naive" 

The probability under the question is  5%2F15 = 1%2F3.    ANSWER

2-nd way - Formal 

    The probability to have the sum >= 8  

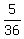        P1 = P( sum >= 8) = 15%2F36;


    The probability to have the sum >= 8 AND at least one component 4  

        P2 = P(sum >= 8 AND at least one component 4) = 5%2F36;


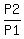     Therefore, the conditional probability under the question is  P = P2%2FP1 = %28%285%2F36%29%29%2F%28%2815%2F36%29%29 = 5%2F15 = 1%2F3.    ANSWER

Solved.