Question 1137735: Using the standard normal table, the total probabilities to the right of z=2.18 and to the left of z=-1.75
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the standard normal table that i use can be found by clicking on the followijng link.
https://www.math.arizona.edu/~rsims/ma464/standardnormaltable.pdf
the table is designed to give you the area to the left of the indicated z-score.
to get the area to the right of the indicated z-score, you would take the area to the left of the indicated z-score and subtract it from 1.
from the table, .....
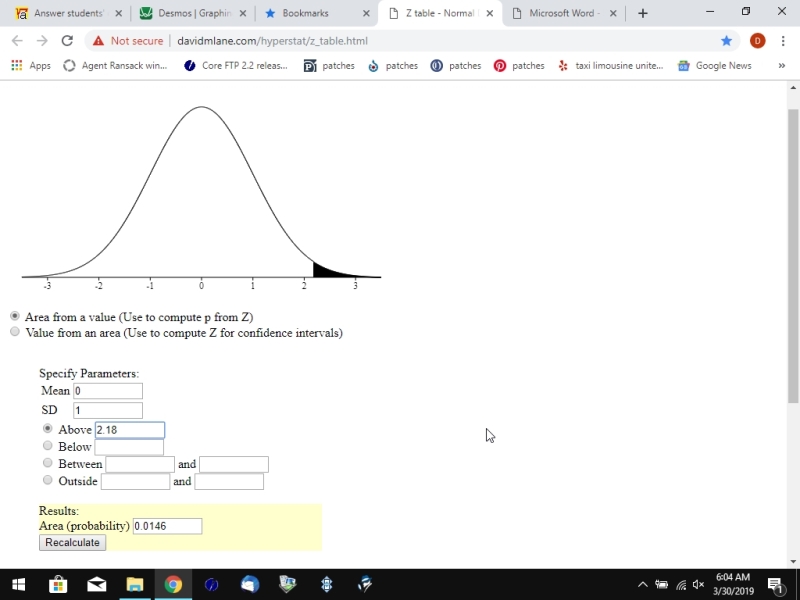
area to the left of the z-score of 2.18 is equal to .98537.
area to the left of the z-score of -1.75 is equal to .04006.
since the area to the right is equal to 1 minus the area to the left, then .....
area to the right of the z-score of 2.18 is equal to 1 minus .98537 = .01463.
area to the right of the z-score of -1.75 is equal to 1 minus .04006 = .95994.
because the normal distribution table is symmetric about the mean, you get the following relationships.
area to the left of the mean is .5 and area to the right of the mean is .5.
in other words, the mean is exactly in the middle of the normal distribution, as is the median and the mode.
the area to the left of 2.18 is the same as the area to the right of -2.18.
the area to the left of -1.75 is the same as the area to the right of 1.75.
the area to the left of a z-score is the probability that a z-score will be less than the indicated z-score.
the area to the right of a z-score is the probability that a z-score will be greater than the indicated z-score.
for example, the z-sore of 2.18 has an area to the left of it equal to .98537 and an area to right of it equal to .01463.
what this says is that the probability of getting a z-score less than 2.18 is .98537 and the probability of getting a z-score greater than 2.18 is .01463.
z-scores and raw scores are related in the following manner.
z = (x - m) / s
z is the z-score
x is the raw score
m is the raw mean.
s is the standard deviation.
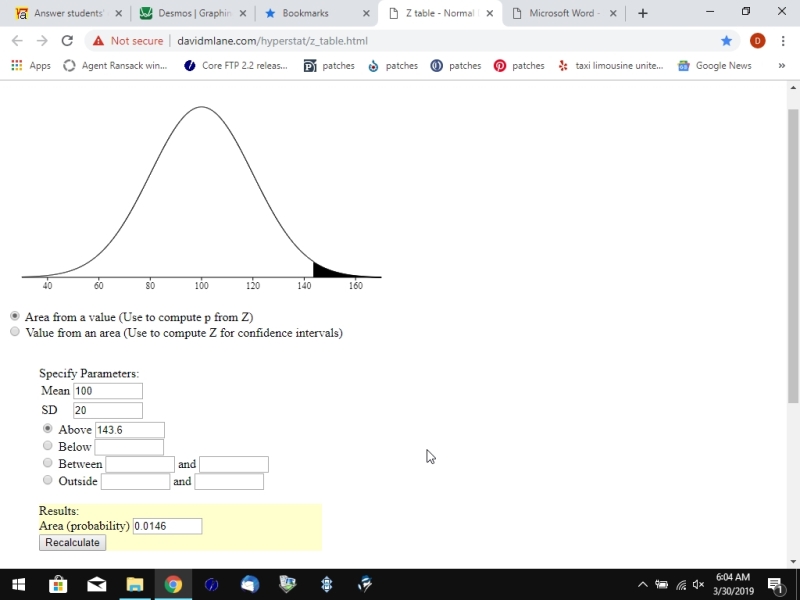
if you have a z-score of 2.18 and the mean of your distribution is 100 and the standard deviation of your distribution is 20, then you can find the raw score associated with that z-score by using the above formula.
the formula becomes 2.18 = (x - 100) / 20.
solve for x to get x = 2.18 * 20 + 100, resulting in x = 143.6.
this tells you that a raw score of 143.6 is 2.18 standard deviations above the mean when the mean is 100 and the standard deviation is 20.
this can be seen visually using the following normal distribution calculator.
http://davidmlane.com/hyperstat/z_table.html
when you use this calculator with z-scores, the mean is 0 and the standard deviation is 1.
when you use this calculator with raw scores, the mean is the mean and the standard deviation is the standard deviation.
here's the displays.
|
|
|