Question 1137583: Find the remainder when 4^503 is divided by 255
Found 4 solutions by math_helper, Edwin McCravy, ikleyn, AnlytcPhil:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Applying Euler's Theorem:
 (mod 255) (mod 255)

so
 (mod 255) (mod 255)
sorry ... pressed Post Answer too soon
I had hoped to use Euler's Theorem to reduce the exponent to something small. However for this problem one ends up with 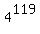 (mod 255) (mod 255)
(119 = 503-128*3), and now the computation of 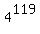 is still too large. is still too large.
Just to finish the thought... the method to reduce 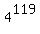 (mod 255) (mod 255)
is to factor 255 into 3*5*17 and then apply Euler's Theorem to each of these.
Once that is done, you will have a set of three modulo congruences which may be solved using the Chinese Remainder Theorem.
Phi(3) = 2 [ Phi(prime) = prime - 1, always ]
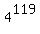 (mod 3) = (mod 3) = 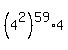 (mod 3) = (mod 3) = 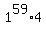 (mod 3) = 4 (mod 3) = 1 (mod 3) (mod 3) = 4 (mod 3) = 1 (mod 3)
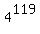 (mod 5) = (mod 5) = 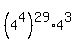 (mod 5) = 64 (mod 5) = 4 (mod 5) (mod 5) = 64 (mod 5) = 4 (mod 5)
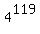 (mod 17) = (mod 17) =  (mod 17) = 13 (mod 17) (mod 17) = 13 (mod 17)
This leads to the set of congruences
13+17n = 13 (mod 17) = 4 (mod 5) = 1 (mod 3)
This can be solved piecewise, algebraically, but since modulus is only 255, you can just list remainder values (mod 255) starting with the largest prime factor to make the list shorter:
13, 30, 47, 64, 81, 98, 115, 132, 149, 166, 183, 200, 217, 234, 251
then list the mod 5 values for these:
3, 0, 2, 4, 1, 3, 0, 2, 4, 1, 3, 0, 2, 4, 1
then list the mod 3 values:
1 0 2, 1, 0, 2, 1, 0, 2, 1, 0, 2, 1, 0, 2
Then notice 64 is the only value satisfying all 3 conditions. The solution is unique, so in practice, if you were listing out the 13 (mod 17) values in the first row, you could check the (mod 5) and (mod 3) values then stop at 64.
------------
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I have much more simple solution.
First, notice that 255 = 256 - 1 = 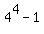 , so , so 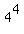 = 255 + 1.
Second, notice that = 255 + 1.
Second, notice that 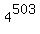 = = 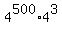 = = 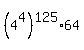 .
Therefore, .
Therefore, 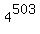 = = 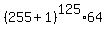 .
Apply the Newton's binomial formula to present .
Apply the Newton's binomial formula to present 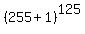 as the sum of degrees of the number 255 with integer coefficients.
All the terms of this binomial expansion will have the number 255 in positive degrees, except the last term, which is 1.
So, all the terms of this binomial expansion are divisible by 255, except the last term 1.
It means that when you multiply this expansion by 64, all the terms of this new expansion are divisible by 255,
except the last term, which is 64.
It proves that the reminder of as the sum of degrees of the number 255 with integer coefficients.
All the terms of this binomial expansion will have the number 255 in positive degrees, except the last term, which is 1.
So, all the terms of this binomial expansion are divisible by 255, except the last term 1.
It means that when you multiply this expansion by 64, all the terms of this new expansion are divisible by 255,
except the last term, which is 64.
It proves that the reminder of 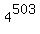 is 64, when it is divided by 255. is 64, when it is divided by 255.
Solved.
-------------
By the way, it is a STANDARD method for solving such problems.
It works smoothly in many other similar problems.
Answer by AnlytcPhil(1810)   (Show Source): (Show Source):
You can put this solution on YOUR website! I think the straight-forward way, i.e.,
"divide it out and see what the remainder is"
is the best way:
4⁴⁹⁹ + 4⁴⁹⁵ + ... + 4⁷ + 4³
4⁴-1)4⁵°³
4⁵°³-4⁴⁹⁹
4⁴⁹⁹
4⁴⁴⁹ - 4⁴⁹⁵
4⁴⁹⁵
...
4⁷
4⁷ - 4³
4³ = R
Edwin
|
|
|