Question 1136120: A batch of 5000 electric lamps has a mean life of 1000 hours and a standard deviation of 75 hours. Assuming a normal distribution:
1.1 how many lamps will fail before 900 hours?
1.2 how many lamps will fail between 950 and 1000 hours?
1.3 and given the same mean life, what would the standard deviation have to be to ensure that not more than 20% OF LAMPS FAIL BEFORE 916 HOURS?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you can use the normal distribution tables or you can use a normal distribution calculator that looks up the values for you and gives you a more accurate answer.
i would recommend using a calculator unless you absolutely have to use the tables.
one of the online calculators i use for this purpose can be found at https://stattrek.com/online-calculator/normal.aspx
the fields in this calculator are shown below.
i will refer to them, from top to bottom, as the x field, the p field, the m field, and the s field.
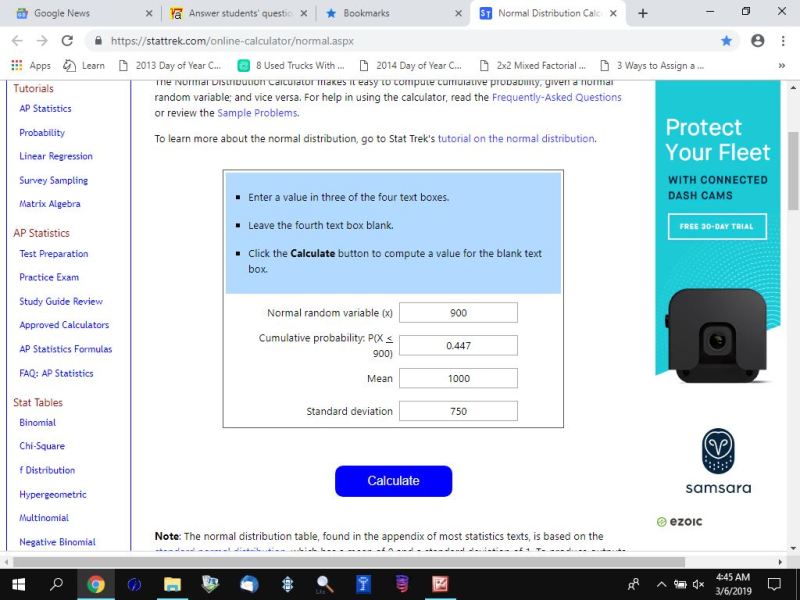
to solve your first problem, enter 900 in the x field and leave the p field blank and enter 1000 in the m field and 750 in the s field.
hit the calculate button and the calculator will tell you that the area to the left of 900 is equal to .447.
that's the probability that the life of a rndomly chosen bulb will be less than 900 if the mean is 1000 and the standard deviation is 750.
to solve your second problem, you need to find the area to the left of 950 and the area to the left of 1000 and subtract the smaller area from the larger area to get the area in between.
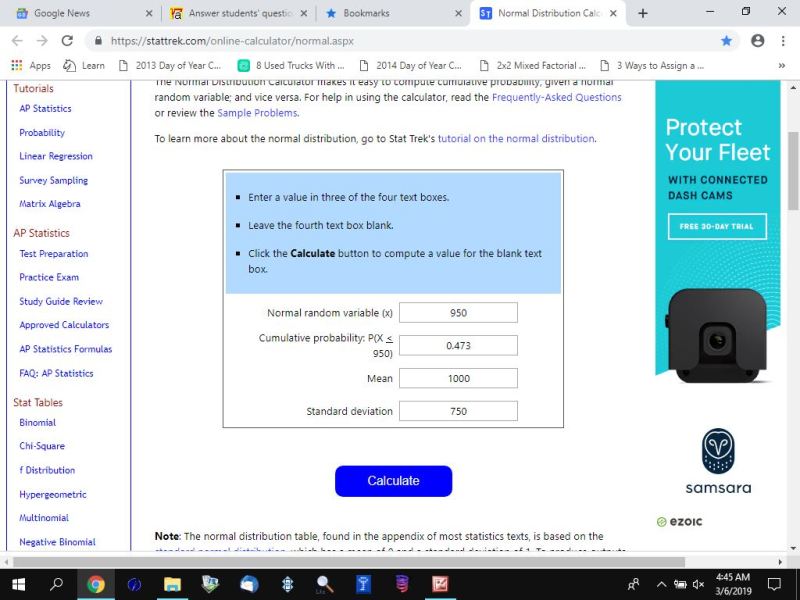
to get the area to the left of 950, you set x to 950 and clear p and set m to 1000 and s to 750.
click on calculate and the calculator will tell you that the area to the left of 950 is equal to .473
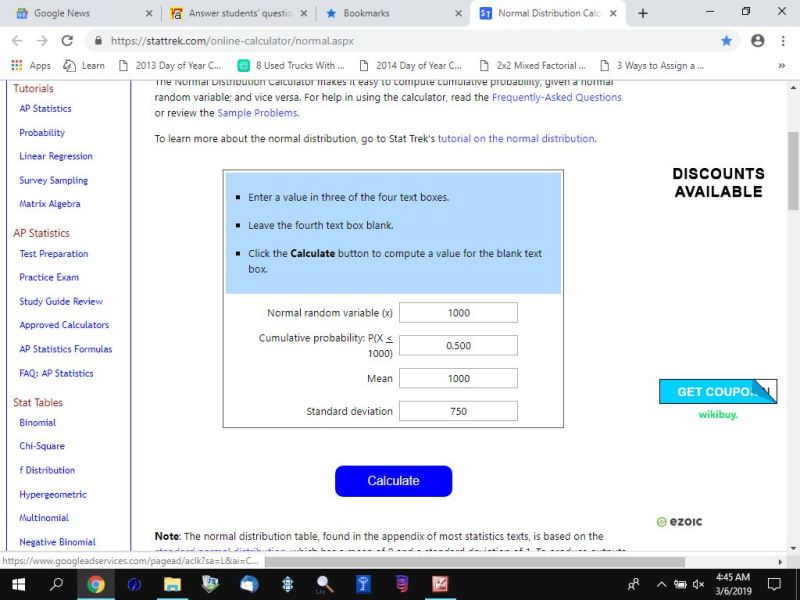
to get the area to the left of 1000, you set x to 1000 and clear p and m to 1000 and s to 750.
click on calculate and the calculator will tell you that the area to the left of 1000 is equal to .5.
subtract the smaller area from the larger area to get .5 minus .473 = ..027.
that's the probability that the life of a randomly chosen bulb will be between 950 and 1000 hours.
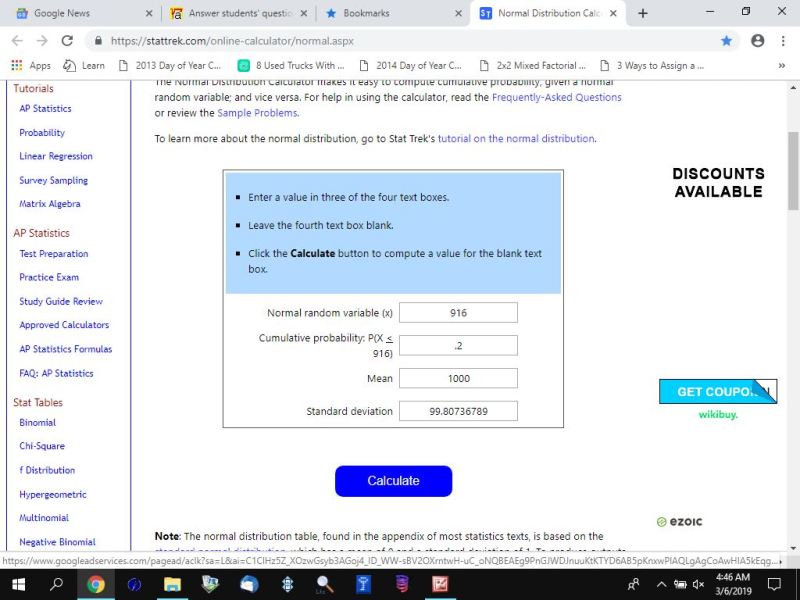
to find the standard deviation that will tell you that the area to the left of 916 is .2, you set the x field to 916 and the p field to .2 and the m field to 1000 and clear the s field.
click on calculate and the calculator will tell you that the standard deviation needs to be 99.80736789.
when the mean is 1000 and the standard deviation is 99.80736789, the probability that the life or a randomly chosen bulb will be less than 916 hours is .20.
to determine how many lamps are involved, you multiply the probability by the total number of bulbs.
the number of bulbs with a life less than 900 will be equal to .447 * 5000 = 2235.
the number of bulbs with a life between 950 and 1000 hours will be equal to .027 * 5000 = 135.
the number of bulbs with a life less than 916 when the standard deviation is equal to 99.80736789 will be .2 * 5000 = 1000.
|
|
|