Question 1126217: The function f is defined as f(x)=(x-2)(x+4)^2. Answer the following questions without using a graphing calculator.
a. Use algebraic methods to determine the roots of f.
b. On what interval(s) of x is f(x)positive? (Hint: enter "U" for U to combine more than one interval.)
c On what interval(s) of x is f(x) negative? (Hint: enter "U" for U to combine more than one interval.)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! set f(x) = 0 and you get (x-2) * (x+4)^2 = 0
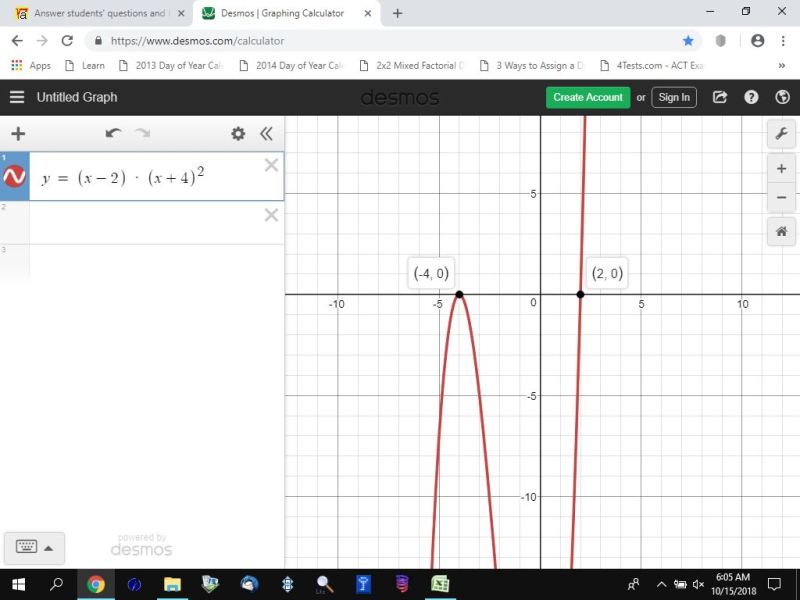
the roots are x = 2 and x = -4.
f(x) = 0 when x = 2 and x = -4
the intervals between these zero points are:
(-infinity,-4) which means x is smaller than -4.
(-4,2) which means x is greater than -4 and less than 2.
(2,+infinity) which means x is greater than 2.
since the function is continuous, if x is smaller than 0 in an interval, it will stay smaller than x for the whole interval and, if x is greater than 0 in an interval, it will stay greater than 0 for the hole interval.
pick any value in each interval to test whether the function is positive or negative in that interval.
for the interval where x is less than -4, i chose -5.
f(x) = (x-2) * (x+4)^2 becomes f(x) = -7 * 1 which becomes f(x) = -7 which is negative.
for the interval where x is greater than -4 but less than 2, i chose 0.
f(x) = (x-2) * (x+4)^2 becomes f(x) = -2 * 16 which becomes f(x) = -32 which is negative.
for the interval where x is greater than 2, i chose 5.
f(x) = (x-2) * (x+4)^2 becomes f(x) = 3 * 81 which becomes f(x) = 243 which is positive.
the function is negative when x < -4 and when -4 < x < 2.
the function is positive when x > 2.
i interval notation, this results in:
the function is negative during the interval (-infinity, -4) union (-4, 2).
the function is positive during the interval (2, +infinity).
the graph of the function confirms this analysis is true, as shown below.
|
|
|