SOLUTION: The names of four students are placed in a small box and two will be selected. Let 1, 2, 3 and 4 denote the students. What is the probability that: a) 3 is selected? b) 3 or 4 is

    In all, there are 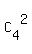  = 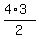 = 6 groups of 2 students, that can be formed of 4 students.

    Of these 6 groups, exactly 3 groups contain "3".  They are  (3,1), (3,2), and (3,4).

    Thus the probability under the question a) is   = .

    There is ONLY ONE group of two students, which contain NEITHER "3"  NOR  "4".

    This group is (1,2).

    The rest 5 of 6 groups necessary / inevitably contain  EITHER "3"  OR  "4".

    Thus the probability under the question b) is  .

    As we saw in the n. a), there are 3 groups of two students that contain "3".

    Hence, of the total possible 6 groups three contain "3", while 3 other do not.

    Thus the probability under the question c) is   = .