SOLUTION: Please help me solve this in simple way. A quick quiz consists of 3 multiple choice problems, each of which has 5 answers, only one of which is correct. If you make random gues

    Imagine that for each of the 3 multiple choice question the answers are labeled by 5 letters A, B, C, D and E  

    (5 possible answers to each question).

     By answering to each question, you mark your answer by one of the 5 letters.

     So, by answering to 3 questions, you write the word of the length 3, using one of 5 letters in each of the three positions.


     It is your model. The entire space of events consists of all 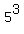 = 125 such words of the length 3, written in 5-letter alphabet.


         Now we are ready to answer the problem's questions.

     If all 3 of your answers are incorrect, it means that in each of the 3 positions you put one of 4 letters, distinct of correct.

     You can do it in   ways, therefore, the probability under the question is 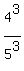  =  =  = 0.512.

     If all 3 of your answers are correct, it means that in each of the 3 positions you guessed the correct letter.

     There is ONLY ONE way to do it; therefore, the probability under the question is   = 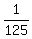 = 0.008.