SOLUTION: Two containers A and B are different. The Container A contains three white balls and two red balls and container B contains only one white ball. A coin is thrown and if faced, a ba

Algebra ->  Probability-and-statistics -> SOLUTION: Two containers A and B are different. The Container A contains three white balls and two red balls and container B contains only one white ball. A coin is thrown and if faced, a ba      Log On


   

Question 1119657: Two containers A and B are different. The Container A contains three white balls and two red balls and container B contains only one white ball. A coin is thrown and if faced, a ball is randomly withdrawn from container A and placed in container B, but if it yields a crown, then two balls are randomly withdrawn from container A and placed in container B. Now a ball is withdrawn randomly from container B. Question: Which the probability of the ball to be white?
Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let's analyse first what will happen, when the coin is faced up. 

1.  With the probability of 1/2 the coin is faced up.


        Then  with the probability 3/5 White ball goes from A to B, making B-content equal to (2W,0R),

          OR  with the probability 2/5  Red ball  goes from A to B, making B-content equal to (1W,1R).


    Summary for this step:

            With the probability (1/2)*(3/5) = 3/10 the content of B becomes (2W,0R)    (1a)    and/or

            with the probability (1/2)*(2/5) = 2/10 the content of B becomes (1W,1R).   (1b)


     Next step is to withdraw the ball from B. 

          In case (1a) we withdraw White ball with the probability 1.

          In case (1b) we withdraw White ball with the probability 1/2.


     Thus the final probability to have White ball as the final outcome at this consideration is

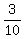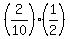         3%2F10%29%2A1 + %282%2F10%29%2A%281%2F2%29 = 3%2F10+%2B+1%2F10 = 4%2F10.  (*)


The analysis for the coin faced up is completed.


Next we analyse what will happen, when the coin is crowned up. 

2.  With the probability of 1/2 the coin is crowned up.


        Then  with the probability 3/10 2 White balls go from A to B, making B-content equal to (3W,0R),

          OR  with the probability (1/3)*(1/2)  1 White ball and 1 Red ball   go from A to B, making B-content equal to (2W,1R),

          OR  with the probability (1/10)  2 Red balls   go from A to B, making B-content equal to (1W,2R).


    Summary for this step:

            With the probability (1/2)*(3/10) = 3/20 the content of B becomes (3W,0R),        (2a)    and/or

            with the probability (1/2)*(1/3)*(1/2) = 1/12 the content of B becomes (2W,1R),   (2b)    and/or

            with the probability (1/2)*(1/10) = 1/20 the content of B becomes (1W,2R).        (2c)  


     Next step is to withdraw the ball from B. 

          In case (2a) we withdraw White ball with the probability 1.

          In case (2b) we withdraw White ball with the probability 2/3.

          In case (2c) we withdraw White ball with the probability 1/3.


     Thus the final probability to have White ball as the final outcome at this consideration is

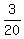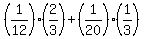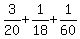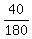         3%2F20%29%2A1 + %281%2F12%29%2A%282%2F3%29+%2B+%281%2F20%29%2A%281%2F3%29 = 3%2F20+%2B+1%2F18+%2B+1%2F60 = 27%2F180+%2B+10%2F180+%2B+3%2F180 = 40%2F180.   (**)


The analysis for the coin crowned up is completed.


The last step to complete the solution is to add  (*)  and  (**) : 

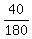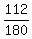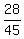    4%2F10 + 40%2F180 = 72%2F180+%2B+40%2F180 = 112%2F180 = 28%2F45 = 0.6222 = 62.22% (approximately).

Answer.   The probability to withdraw white ball is 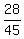  28%2F45 = 0.6222 = 62.22%  (approximately).