Question 1119602: There are 6 people who will sit in a row but out of them James will always be left of Esther and John will always be right of Esther. In how many ways such arrangement can be done?
Note: i tried solving and got 24 as the answer but there was no 24 in the options. here are the options:
120
72
64
218.
Many thanks.
Found 3 solutions by solver91311, ikleyn, greenestamps:
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website!
I know why you got 24 as an answer, and I know why that answer is incorrect. You apparently assumed that "James will always be left of Esther and John will always be right of Esther" meant that James is always to the IMMEDIATE left of Esther and that John is always to the IMMEDIATE right of Esther. However, that is not what the problem actually says. I'm sure there is a more elegant way of calculating this that I am missing, but here is how I came up with the answer:
First, consider all possible arrangements where James is the very first person in the row from left to right and Esther is seated next to him:
J E J _ _ _
J E _ J _ _
J E _ _ J _
J E _ _ _ J
Notice that for each of the above configurations, there are 6 different ways to arrange the other three people. Now move Esther one seat to the right:
J _ E J _ _
J _ E _ J _
J _ E _ _ J
Again, for each configuration, there are 6 different ways to arrange the other three people. So continue on moving Esther one seat to the right until you run out of possibilities. Count the number of configurations and multiply by 6. If you do this carefully, you will obtain one of the numbers on your list.
John
My calculator said it, I believe it, that settles it
Answer by ikleyn(52777)  (Show Source):
You can put this solution on YOUR website! .
I will provide here another solution.
Probably, it is that "elegant" solution John mentioned in his post.
For each given arrangement from the condition, consider all 6 (six) permutations of the three people James, Esther and John
inside of the greater arrangement.
In this way, you will get all possible 6! = 1*2*3*4*5*6 = 720 arrangements of 6 people in a row.
Therefore, the number of all arrangements under the problem's question is 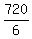 = 120.
Answer. The number of all arrangements under the problem's question is 120.
-------------------
Comment from student: thank you so much Ikleyn. i so much appreciate. i have liked and recommended your page to my friends.
pls i still have one more.
Dada want to change her password which is dada112233 but with same letters and number. In how many ways she can do that? thank you in anticipation.
-------------------
My responce. Although it is not formulated explicitly and directly in the condition, I will assume that
4 letters occupy 4 first positions, and
6 digits occupy the last 6 positions.
So, we have all distinguishable arrangements of the word "dada" in the first 4 positions and all distinguishable arrangements
of 6 digits "112233" in the last 6 positions.
The word "dada" has 4 letters in all; of them, there are only 2 distinguishable letters each of the multiplicity 2.
The number of all distinguishable arrangements for letters is  =  = 6 in this case.
(2!*2!) in the denominator stays to account for repeated "a" and repeated "d" with their multiplicities.
The word "112233" has 6 digits in all; of them, there are only 3 distinguishable digits each of the multiplicity 2.
The number of all distinguishable arrangements for digits is 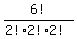 =  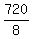= 90 in this case.
(2!*2!*2!) in the denominator stays to account for repeated "1"; repeated "2", and repeated "3" with their multiplicities.
Now, to complete the solution, we need simply multiply 6 by 90.
Answer. There are 540 different ways to create the password in a way described in the problem.
See the lesson
- Arranging elements of sets containing indistinguishable elements
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
=============
In the future, when you post your message through the "Thank you/comment" window, following my post, please refer
to the problem ID number (which is "1119602" in this case)
in order I could identify the problem properly and answer under the appropriate post.
Thank you.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
Here is another way to solve the problem.
(1) Place James, Esther, and John in the proper order.
(2) Have the 4th person choose a place in the line. With 3 people currently in the line, there are 4 choices for where he can stand (left of James, between James and Esther, between Esther and John, or right of John).
(3) Now there are 4 people in line; the 5th person has 5 choices of where to stand in the line.
(4) Now there are 5 people in the line; the last person has 6 choices of where to stand in the line.
The total number of different arrangements with the given restrictions is the product of the numbers of choices the last three people had for where to stand in the line: 4*5*6 = 120.
|
|
|
