Question 1118905: The time it takes me to wash the dishes is uniformly distributed between 11 minutes and 21 minutes.
What is the probability that washing dishes tonight will take me between 13 and 19 minutes?
Found 3 solutions by Theo, ikleyn, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i think the answer will be as follows:
if it takes between 11 and 21 minutes, then the possible number of minutes that it could take would be 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21.
that's a total of 11 separate and discrete minutes in that interval.
if it takes between 13 and 19 minutes, then the possible minutes that it could take would be 13, 14, 15, 16, 17, 18, 19.
that's a total of 7 separate and discrete minutes in that interval.
the probability of it taking between 13 and 19 minutes is therefore 7/11 = .6363 rounding to 4 decimal places which is equal to 63.63% rounding to 2 decimal places.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Time interval duration "between 11 minutes and 21 minutes" is 10 minutes:
1 minute from 11 min. to 12 min.
1 minute from 12 min. to 13 min.
1 minute from 13 min. to 14 min.
1 minute from 14 min. to 15 min.
1 minute from 15 min. to 16 min.
1 minute from 16 min. to 17 min.
1 minute from 17 min. to 18 min.
1 minute from 18 min. to 19 min.
1 minute from 19 min. to 20 min.
1 minute from 20 min. to 21 min.
Time interval duration "between 13 minutes and 19 minutes" is 6 minutes:
1 minute from 13 min. to 14 min.
1 minute from 14 min. to 15 min.
1 minute from 15 min. to 16 min.
1 minute from 16 min. to 17 min.
1 minute from 17 min. to 18 min.
1 minute from 18 min. to 19 min.
The probability under the question is the ratio of 6 minutes to 10 minutes  = 0.6 = 60%. = 0.6 = 60%.
Solved.
The solution and the answer by the other tutor are incorrect.
=================
After reading the @greenestamps solution I added this NOTICE.
The meaning of this problem is THIS:
I have a stop watch. I turn it on when I start dish washing, and I stop it when the process ends.
I write the reading of the stop watch after every/each experiment.
Then I see that the readings for the process duration are uniformly distributed over the time interval between 11 minutes
(=from the start of the 11-th minute reading) and 21 minutes (=to the complete end of the 20-th minute,
i.e. to the moment, when 21-th minute starts).
. . . And so on to the end of the condition.
This problem HAS THIS and ONLY THIS reading and meaning.
Nothing else. // The words "uniformly distributed" of the condition do not leave the place (the gap) for any other interpretation.
Any different interpretation is FALSE and IRRELEVANT.
In particular, the proposed by @greenestamps interpretation is wrong.
I agree that the problem formulation is not perfect, since it does not determine if 21-th minute is included completely or not.
If it is included (as well as the 19-th minutes is fully included), then the answer is 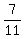 . .
But in any case two continuous time intervals are considered, and there is no place for a "discrete" interpretation.
----------------
It is a STANDARD introductory problem on geometric probability.
To see other similar solved problems, look into the lesson
- Geometric probability problems
in this site.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It's probably wrong of tutor @ikleyn to say the solution by the other tutor @theo is wrong.
It seems LIKELY that the intent of the problem is to treat the time between 11 and 21 minutes as a continuous range of 10 minutes; however, it could be that the data points are expressed to the nearest minute, making the data values the 11 discrete values 11, 12, ..., 21, making the solution by tutor @theo valid.
So the statement of the problem is unclear enough to allow different interpretations.
|
|
|