Question 1111413: I need help figuring out how to get the new grade by using the z score of the new mean. Help please!
Suppose a professor gives an exam to a class of 40 students and the scores are as follows.
35 44 46 47 47 48 49 51 53 54
55 55 57 57 57 58 59 59 59 59
60 60 60 60 60 62 62 62 64 68
69 70 72 73 73 75 75 77 82 88
Question....
3. Suppose the professor wants the final scores to have a mean of 75 and a standard deviation of 8.
To find a studentís new score, first calculate their z-score and then use the z-score along with the new mean and standard deviation to find their adjusted score. re-type the new scores below.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i think what they're asking is the following.
the mean of the original data set is 60.525 and the standard deviation of the original data set is 10.818935945831.
the raw score of 35 would have a z-score of (35 - 60.525) / 10.818935945831, which is equal to -2.821441975
that z-score with a data set that has a mean of 75 and a standard deviation of 8 would have a raw score of -2.821441975 * 8 + 75 = 52.4284642
the formula to use for z-score is:
z = (x - m) / s
z is the z-score
x is the raw score of the data set
m is the mean of the data set
s is the standard deviation of the data set.
if you know the z-score, you can use the z-score formula to find the raw score.
the formula to find the raw score, derived from the formula for the z-score, is:
x = z * s + m
assuming the z-score is -2.821441975 and the standard deviation is 10.818935945831 and the mean is 60.525, you would calculate the raw score as:
x = z * s + m.
this makes x = -2.821441975 * 10.818935945831 + 60.525 which results in:
x = 35.
this makes sense, since we started with a raw score of 35 and calculated the z-score of -2.821441975 from the mean of the original data set of 60.525 and the standard deviation of the original data set of 10.818935945831.
that same z-score, however, when it is part of a data set that has a mean of 75 and a standard deviation of 8 would generate a raw score as shown below.
x = -2.821441975 * 8 + 75 which makes the raw score equal to 52.4284642.
52.4284642 is the same number of standard deviations below the mean of 75 with a standard deviation of 8 as 35 is below the mean of 60.525 with a standard deviation of 10.818935945831.
since there was a large number of calculations, i did them in excel.
the following is the result of the excel calculations.
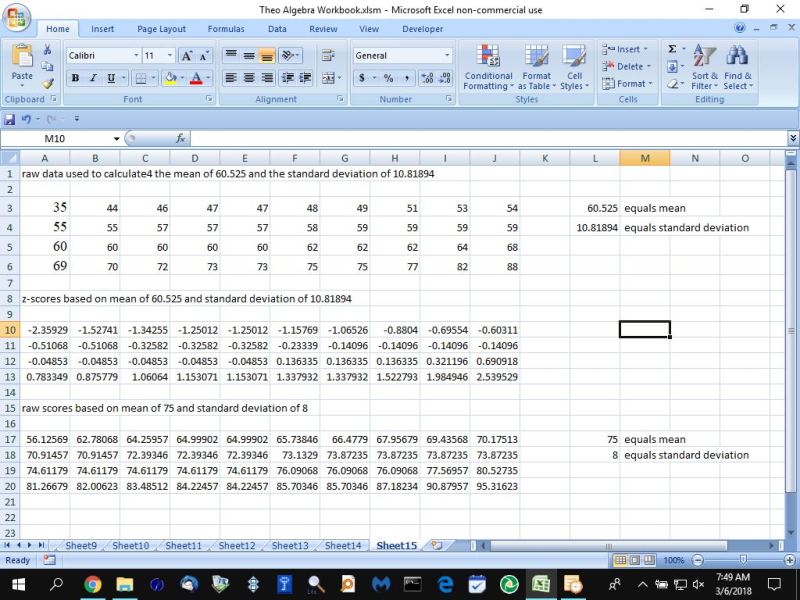
the first set of data are the original scores that were used to find the mean of 60.525 and the standard deviation of 10.818935945831.
the second set of data was the z-score derived from the original set of data and its associate mean and standard deviation.
the third set of data was the raw scores derived from the z-scores with a data set that has a mean of 75 and a standard deviation of 8.
|
|
|