Question 1105966: I do not know how they got the answer
Three dice are rolled. Find each probability:
a) One of the rolls is a 6, given all rolls are even. ans. 12/27
b) One of the rolls is a 3, given two rolls are even. ans. 4/9
c) At least two of the rolls are even, given all three rolls are the same. ans. 1/2
Found 2 solutions by rothauserc, KMST:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) given all three rolls are even and there are three possibilities
6XX = (1/3) * (2/3) * (2/3) = 4/27
X6X = (2/3) * (1/3) * (2/3) = 4/27
XX6 = (2/3) * (2/3) * (1/3) = 4/27
Probability (P) (One of the rolls is a 6, given all rolls are even) = 3(4/27) = 12/27
:
can you now do the others?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is my conclusion:
a) If all rolls are even, there is exactly one roll that is a 6 in  of the equally possible cases. of the equally possible cases.
b) If exactly two rolls are even, there is exactly one roll that is a 3 in  of all equally possible cases. of all equally possible cases.
The only place where I get a  is the probability of rolling exactly one 3, when exactly two of the numbers rolled were odd. is the probability of rolling exactly one 3, when exactly two of the numbers rolled were odd.
c) At least two of the rolls are even, If all three rolls are the same, all rolls are even in 1/2 of all 6 possible cases, and all rolls are odd in the other 1/2 of all 6 possible cases. That means that  of the 6 cases where all rolls are the same have at least two of the rolls that are even (and all rolls are even in those cases. of the 6 cases where all rolls are the same have at least two of the rolls that are even (and all rolls are even in those cases.
How I got those answers:
a) If a roll of one die is an even number, a 6 is as likely as a 4 or a 2,
so there are  equally likely possibilities for each die. equally likely possibilities for each die.
One way to "show your work" is to say that with an even roll,
the probability of 6 is is  and and  . .
For one die, those probabilities are represented by the corfficients of  and and  in in 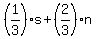 . .
You would then say that applying binomial distribution probability,
with  dice being rolled, the probability of exactly dice being rolled, the probability of exactly  6 is 6 is
the coefficient in the term with  in the expansion of in the expansion of
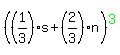 . .
That expansion is
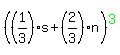  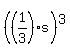  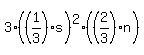  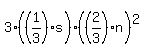  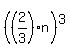  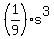  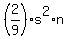  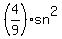  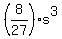 . .
Another way would involve calculating counts (or literall ycounting):
With three dice, you would have
 equally likely possibilities (outcomes). equally likely possibilities (outcomes).
You could similarly calculate the different kinds of outcomes as
 of those of those  equally likely outcomess would be a 6 from all 3 dice (three 6's), equally likely outcomess would be a 6 from all 3 dice (three 6's),
 would be one of the would be one of the  even rolls being one of the even rolls being one of the  non-6 even numbers (two 6's), non-6 even numbers (two 6's),
 would be all would be all  rolls being one of the rolls being one of the  non-6 even numbers (no 6"s), non-6 even numbers (no 6"s),
and the remaining  would be exactly one 6 rolled. would be exactly one 6 rolled.
You can also calculate that  (the number of "favorable outcomes") as (the number of "favorable outcomes") as
 places to put the one 6, places to put the one 6,
times  possibilities for the two other non-6 even numbers rolled. possibilities for the two other non-6 even numbers rolled.
Dealing with such a small total number of equally likely outcomes,
you could literally count them.
You can list them as 3 digit numbers,
where each digit position would represent the result of rolling one specific die.
Then you could literally count outcomes.
You could distinguish the three dice by colors
(as the red die, the white die, and the blue dice, listed in that order),
or you could distinguish the dice by when and where they were rolled.
The sequences of 3 (all even) numbers rolled
(by the first second and third die rolled, in that order) can be listed as

There are  outcomes, outcomes,
and  of them have exactly one 6, of them have exactly one 6,
so the probability of getting exactly one 6 when the 3 dice rolls are even is
 . .
b) If two of the 3 rolls are even, and the other roll is odd,
the situation is the same for any die the odd roll comes from,
and for any arrangement of even numbers rolled by the other two dice.
There are 3 possibilities for the odd roll: 1, 3, or 5.
Each odd number will be in  of the two-even-one-odd rolls. of the two-even-one-odd rolls.
We do not even need to calculate or count outcomes, but here it goes.
There are  odd numbers that could be the odd roll. odd numbers that could be the odd roll.
There are  dice that could be the odd roll. dice that could be the odd roll.
There are  possible even numbers that could be rolled possible even numbers that could be rolled
for each of the other  dice. dice.
That makes for  different outcomes. different outcomes.
Of those,  would include rolling a 3. would include rolling a 3.
 . .
What about counting all outcomes to make sure that is right?
I had my computer do it with a spreadsheet .
Of the  possible outcomes of rolling 3 dice, possible outcomes of rolling 3 dice,
There were  different, equally likely, all-odd outcomes, different, equally likely, all-odd outcomes,
 different, equally likely, all-even outcomes, different, equally likely, all-even outcomes,
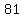 different, equally likely, two-even-one-odd outcomes, different, equally likely, two-even-one-odd outcomes,
and 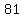 different, equally likely, two-odd-one-even outcomes. different, equally likely, two-odd-one-even outcomes.
Of the 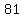 two-even-one-odd outcomes, two-even-one-odd outcomes,  included rolling one 3. included rolling one 3.
c) All three rolls being the same includes 6 different, equally likely outcomes:
all rolls are 1, all are 2, all are 3, all are 4, all are 5, and all are 6.
In  of those of those  cases, the number on all 3 dice is even, cases, the number on all 3 dice is even,
and in for the other 3 all-rolls-the-same, the number on all 3 dice is
That is, in  of the outcomes considered, 3 rolls are even, of the outcomes considered, 3 rolls are even,
and in  of the outcomes considered, 3 rolls are odd. of the outcomes considered, 3 rolls are odd.
In other words, in  of the outcomes considered, none of the numbers rolled is even, of the outcomes considered, none of the numbers rolled is even,
and the other  of the outcomes considered, of the outcomes considered,
at least 2 of the numbers rolled are even, because all 3 are.
|
|
|