SOLUTION: How many people would you have to have in a group so that there is a probability of at least 0.7 that at least two of them will have the same birthday? and How many people

Let assume that the group consists of n people.



You can write their birthdays in a row, divided by commas.

Then such row will contain n integer numbers (each between 1 and 365) divided by commas.



Your full space of events is the set of all such rows.

In principle, the numbers can repeat in a row.  So, repeating is allowed.

The full number of such rows is 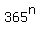   (any of 365 integers from 1 to 365 can stay in any of n positions in a row).



The  complement to the sub-space  the problem is asking for, is the space of rows of the length n  WITHOUT repeating.

The number of such rows is, OBVIOUSLY,  365*364*363* . . . *(365-n+1).



So, the probability under the question is this number

P(n) = 1 - 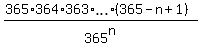,   or, which is the same (but more convenient for calculations)


P(n) = 1 -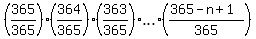 


And the problem asks (question 1) to find n such that  P(n) >= 0.7.



I prepared the table of values for the function P(n) below:


                       TABLE

                Factors         Long        P(n) =
n	365-n+1	(365-n+1)/365	product	    = 1 - long product

1	365	1.0000	        1.0000	
2	364	0.9973	        0.9973	    0.0027
3	363	0.9945	        0.9918	    0.0082
4	362	0.9918	        0.9836	    0.0164
5	361	0.9890	        0.9729	    0.0271
6	360	0.9863	        0.9595	    0.0405
7	359	0.9836	        0.9438	    0.0562
8	358	0.9808	        0.9257	    0.0743
9	357	0.9781	        0.9054	    0.0946
10	356	0.9753	        0.8831	    0.1169
11	355	0.9726	        0.8589	    0.1411
12	354	0.9699	        0.8330	    0.1670
13	353	0.9671	        0.8056	    0.1944
14	352	0.9644	        0.7769	    0.2231
15	351	0.9616	        0.7471	    0.2529
16	350	0.9589	        0.7164	    0.2836
17	349	0.9562	        0.6850	    0.3150
18	348	0.9534	        0.6531	    0.3469
19	347	0.9507	        0.6209	    0.3791
20	346	0.9479	        0.5886	    0.4114
21	345	0.9452	        0.5563	    0.4437
22	344	0.9425	        0.5243	    0.4757
23	343	0.9397	        0.4927	    0.5073
24	342	0.9370	        0.4617	    0.5383
25	341	0.9342	        0.4313	    0.5687
26	340	0.9315	        0.4018	    0.5982
27	339	0.9288	        0.3731	    0.6269
28	338	0.9260	        0.3455	    0.6545
29	337	0.9233	        0.3190	    0.6810
30	336	0.9205	        0.2937	    0.7063    <<<---=== enough for 0.7
31	335	0.9178	        0.2695	    0.7305
32	334	0.9151	        0.2467	    0.7533
33	333	0.9123	        0.2250	    0.7750
34	332	0.9096	        0.2047	    0.7953
35	331	0.9068	        0.1856	    0.8144    <<<---=== enough for 0.8
36	330	0.9041	        0.1678	    0.8322
37	329	0.9014	        0.1513	    0.8487
38	328	0.8986	        0.1359	    0.8641
39	327	0.8959	        0.1218	    0.8782
40	326	0.8932	        0.1088	    0.8912

. . . . . . . . . . . . . . . . . . . 


From the Table, you have THIS 

Answer.  30 people are enough to have the probability at least 0.7.

                
         35 people are enough to have the probability at least 0.8.