Question 1103356: 6 freshmen, 8 sophomores, 10 juniors, and 9 seniors are eligible to be on a committee. If a committee of 14 students is chosen at random, what is the probability that it is made up of 2 freshmen, 3 sophomores, 4 juniors, and 5 seniors?
Even if you don't use the exact problem, it's fine, since I want to learn how to find the probability.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
Okay; I will use different numbers: 4 freshmen, 3 sophomores, 7 juniors, and 7 seniors. And we will still make a committee of 14 with 2 freshmen, 3 sophomores, 4 juniors, and 5 seniors.
The basic definition of probability says that the answer is
(number of ways of choosing 2 of the 4 freshmen AND 3 of the 3 sophomores AND 4 of the 7 juniors AND 5 of the 7 seniors) divided by (the total number of ways of choosing 14 of the total 21 students).
Because the calculations involve choosing among candidates, you will be using the "n choose r" concept repeatedly. Since you are asking this question, I will assume you are familiar with that concept.
The denominator of our probability fraction is the number of ways of choosing 14 of the 21 students: C(21,14).
For the numerator, we have to choose certain numbers of each of the four class levels. So the numerator of the probability fraction will be C(4,2)*C(3,3)*C(7,4)*C(7,5).
C(21,14) = 116280; C(4,2)*C(3,3)*C(7,4)*C(7,5) = 6*1*35*21 = 4410; the probability that the committee has 2 freshmen, 3 sophomores, 4 juniors, and 5 seniors is  to 4 decimal places.
Obviously the process for solving your example will be the same, just with different numbers.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
Let me solve MORE SIMPLE problem for you.
6 freshmen and 8 sophomores are eligible to be on a committee.
If a committee of 5 students is chosen at random, what is the probability that it is made up of 3 freshmen and 2 sophomores?
In all, there are 6 + 8 = 14 students to choose from.
So, there are 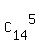 ways to made the committee of 5 students.
It is your TOTAL space of events, and it has 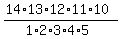 = 2002 elements in all.
Next, in how many ways can you choose 3 freshmen of 6 ? - In 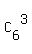 =  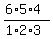= 20 ways.
In how many ways can you choose 2 sophomores of 8 ? - In 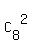 =  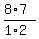= 28 ways.
Thus there are 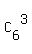. 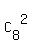= 20*28 = 560 ways to form the committee in accordance with the given requirements.
So, the probability under the question is P =  .
Or, if you want to have it as a "formula", P =  .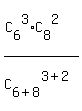
On combinations, see the lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- OVERVIEW of lessons on Permutations and Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|
