SOLUTION: An apartment building has 8 floors. If seven people get on the elevator on the first floor, what is the probability they all want to get off on different floors?

Imagine that all and each floors from 2 to 8 are marked by the first 7 letters of English alphabet:

2  3  4  5  6  7  8
A  B  C  D  E  F  G 


Then the space of all possible events is the set of all 7-letter words comprising of these letters.

Repetitions of letters in these words are allowed.


It is easy to calculate the number of all such 7-letter words.

Any of 7 letter can stay in the 1-st position. This gives 7 opportunities.
Any of 7 letter can stay in the 2-nd position. This gives 7 opportunities.

And so on . . . 

In all, there are  such words.
Correspondingly, there are  elements in the space of events, in all.


Now, the winning events are those 7-letter words what have no repetitions.

The number of such words is exactly  7*6*5*4*3*2*1 = 7! = 5040.



Therefore, the probability under the question is equal to  

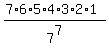 =  =  = 0.00612 = 0.612% (approximately).