SOLUTION: A report in 2010 indicates that Americans between the ages of 8 and 18 spend an average of μ = 10 hours per day using some sort of electronic devices such as smart phones, com

Algebra ->  Probability-and-statistics -> SOLUTION: A report in 2010 indicates that Americans between the ages of 8 and 18 spend an average of μ = 10 hours per day using some sort of electronic devices such as smart phones, com      Log On


   

Question 1094896: A report in 2010 indicates that Americans between the ages of 8 and 18 spend an average of μ = 10 hours per day using some sort of electronic devices such as smart phones, computers, or tablets. Assume that the distribution of times is normal with a standard deviation of σ = 2.5 hours and find the following values.
A. What is the probability of selecting an individual who uses electronic devices more than 12 hours a day?
So far for this one, I have done (9-10)/ 2.5= 1.8. I am not sure what to do from here. I am pretty sure I have to subtract a z score amount from the z table, but I'm not really sure how to figure that out.
B. What proportion of 8- to 18-year-old Americans spend between 8 and 12 hours per day using electronic devices? P(5 I am really confused by this question, I'm not sure where to start.
Found 2 solutions by sophi.riv, ikleyn:
Answer by sophi.riv(1) About Me  (Show Source):
Answer by ikleyn(52777) About Me  (Show Source):
You can put this solution on YOUR website!
.
A report in 2010 indicates that Americans between the ages of 8 and 18
spend an average of μ = 10 hours per day using some sort of electronic devices
such as smart phones, computers, or tablets.
Assume that the distribution of times is normal with a standard deviation
of σ = 2.5 hours and find the following values.
A. What is the probability of selecting an individual who uses electronic devices
more than 12 hours a day?
So far for this one, I have done (9-10)/ 2.5= 1.8. I am not sure
what to do from here. I am pretty sure I have to subtract a z score amount
from the z table, but I'm not really sure how to figure that out.
B. What proportion of 8- to 18-year-old Americans spend between 8 and 12 hours per day
using electronic devices?
P(5 I am really confused by this question, I'm not sure where to start.
~~~~~~~~~~~~~~~~~~~~~


Each normal probability curve is bell shaped curve.

For task (A), you goal is to find the area under this curve on the right
of z-mark 12 hours.

For task (B), you goal is to find the area under this curve between
z-marks 8 and 12 hours.

Each of these areas is the solution/(the answer) to the relevant question.


There are different ways to solve this and similar problems.
I will show/describe some of them in this my post.

                    These ways are

        (1)  using table for cumulative normal distribution function;
        (2)  using calculators like     TI-83     and/or     TI-84.
        (3)  using online calculators from the Internet web-sites.


The best way to start is to use an online calculator from this web-site
https://onlinestatbook.com/2/calculators/normal_dist.html 


So, go to that web-site.

There is an online free of charge calculator there with simple and intuitively clear interface.

In the calculator, input the mean value 10 hours and standard deviation value of 2.5 hours 
in the corresponding port windows.


For question (A), input 12 in the port "Above".
Then click "Recalculate".

You will get the answer 0.2119 for the probability and the corresponding diagram, showing 
the area of interest.


      +----------------------------------------------+
      |    In this way, the problem is just solved,  |
      |    and you just learned your first lesson.   |
      +----------------------------------------------+


Next, if you want to use the table for cumulative normal distribution function,

you should calculate z-score  z = 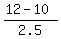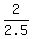%2812-10%29%2F2.5 = 2%2F2.5 = 0.8.

From the table, you will find the corresponding value of the cumulative normal distribution function 0.7881.

    Remember that it is the area to the LEFT of the mark 0.8, 
    while you need the area on the RIGH of this mark.

So, you subtract the value 0.7881 from 1, and you get your answer 1 - 0.7881 = 0.2119,
which is THE SAME, as the online calculator gave you above (!)



And finally, the last way solving with the calculators as TI-83 and/or TI-84.

A function to use in such calculators is normalcdf(z1, z2, mean, SD)  
    // "cdf" stands for cumulative distribution function.


In the calculator, your input is normalcdf(12, 9999, 10, 2.5).

The calculator will give you the answer (the probability) 0.2119.

So,  I answered and explained  EVERYTHING  to you,  which relates to your question  (A).

For instructions on using this function normalcdf,  if you need them,  see the link
https://www.usu.edu/math/cfairbourn/calculatorhelps/normalcdfti-84.pdf

-----------------

In the future,  post your separate questions  SEPARATELY  in separate posts.

It will guarantee you that you will get exhaustive,  exact,  clear answers  (and not a  MESS).