Question 1091943: An octapeptide is known to contain four of one amino acid, two of another and two of third. How many different amino acid sequence are possible?
Found 3 solutions by Fombitz, ikleyn, greenestamps:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An octapeptide is known to contain four of one amino acid, two of another and two of third. How many different amino acid sequence are possible?
~~~~~~~~~~~~~~~~
To correctly answer this question, we need to know what sequences (what connections and interconnections) are allowed.
If ALL sequences and connections are allowed in one-line-arrangement, then the following logic works:
In total, there are 4 + 2 + 2 = 8 amino acid (acids ?).
Anyone of 8 acids can be placed in the 1-st position.
Anyone of remained 7 acids can be placed in the 2-nd position.
Anyone of remained 6 acids can be placed in the 3-rd position.
Anyone of remained 5 acids can be placed in the 4-th position.
. . . . and so on . . . .
Anyone of remaining 2 acids can be placed in the 7-th position.
And there is no choice (except the remained 1 last acid) in the 8-th position.
If this logic is correct from the Chemistry/Biochemistry point of view,
then the answer is 8*7*6*5*4*3*2*1 = 40320 different amino acid sequences are possible.
I am not a Chemist in my education, so my logic easily can be wrong.
It is your responsibility to evaluate if it is True or False.
If it not difficult to you, I would appreciate your feedback, which you can send me through the "Thank you" note.
In this case, please refer to the Problem ID number, which is 1091943.
Thank you and good luck !!
-----------------
From Wikipedia, https://en.wikipedia.org/wiki/Peptide
An octapeptide has eight amino acids (e.g., angiotensin II).
From Wikipedia, https://en.wikipedia.org/wiki/Angiotensin#Angiotensin_II
Angiotensin II
Asp-Arg-Val-Tyr-Ile-His-Pro-Phe | His-Leu
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Sorry to confuse you with (up to now) three different answers to your question....
You are asking for the number of different arrangements of
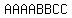
By a well known counting principle, the number of distinct arrangements is

If you aren't familiar with that counting principle, here is a quick explanation....
If all eight items were different, then the number of arrangements would clearly be

Because 4 items are the same, they can be arranged in 4!=24 different ways that are indistinguishable. So we need to divide the number of distinct arrangements by 4!.

Because 2 other items are the same, they can be arranged in 2!=2 different ways that are indistinguishable. So we need to further divide the number of distinct arrangements by 2!.

Finally, because 2 other items are the same, they can be arranged in 2!=2 different ways that are indistinguishable. So we need to further divide the number of distinct arrangements again by 2!.

For another example of the concept, the number of distinct arrangements of the letters MISSISSIPPI (11 letters; 4 the same, 4 others the same, 2 others the same) is
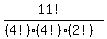
Or...
The number of distinct orders in which you can get 5 heads and 3 tails when you flip a coin 8 times is
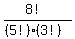
|
|
|