Question 1084227: How many different 5-letter sequences can be made using the first 11 letters of the alphabet? Assume that repetition of letters is allowed.
A.) 55,440
B) 161,051
C) 462
D) 120
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
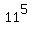 = 161051.
Option B).
Any of 11 letters in the first position gives 11 options.
Any of 11 letters in the second position gives 11 independent options.
. . . and so on . . .
In all, it gives = 161051.
Option B).
Any of 11 letters in the first position gives 11 options.
Any of 11 letters in the second position gives 11 independent options.
. . . and so on . . .
In all, it gives 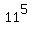 = 161051 5-letter words. = 161051 5-letter words.
Solved.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are 11 ways to choose the 1st letter.
For each of those 11 ways to choose the first letter,
there are 11 ways to choose the 2nd letter.
That's 11×11 or 121 ways to choose the first 2 letters.
For each of those 11×11 or 121 ways to choose the first 2
letters, there are 11 ways to choose the 3rd letter.
That's 11×11×11 or 1331 ways to choose the first 3 letters.
For each of those 11×11×11 or 1331 ways to choose the first
3 letters, there are 11 ways to choose the 4th letter.
That's 11×11×11×11 or 14641 ways to choose the first 4
letters.
For each of those 11×11×11×11 or 14641 ways to choose the
first 4 letters, there are 11 ways to choose the 5th letter.
That's 11×11×11×11×11 or 161,051 ways to choose all 5 letters.
Anawer: 11×11×11×11×11 = 115 = 161,051
Edwin
|
|
|