Question 1075293: And one last question:
A coin is tossed 12 times. Find the probability getting exactly 6 heads.
I know 4096 possibilities... and that is about it :(
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi,
Khan Academy has a great tutorial where they answer the question:
What is the probability of getting exactly 3 heads when you have
5 tosses of a coin. This is the location of the video:
https://www.khanacademy.org/math/precalculus/prob-comb/prob-combinatorics-precalc/v/exactly-three-heads-in-five-flips
---------------------------------------------------
They conclude that the the probability is:
[ number of combinations of ways to get 3 heads in 5 tosses ] / [ 2^5 total possible outcomes ]
or, C( 5,3 ) / 2^5
and
C( 5,3 ) = 
C( 5,3 ) = 
and

-----------------------------------------
If you repurpose this for your problem, you have:
C( 12,6 ) / 2^12
C( 12,6 ) = 
C( 12,6 ) = 
C( 12,6 ) = 
and
C( 12,6 ) / 2^12 = 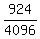
C( 12,6 ) / 2^12 = 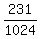
----------------------------------
The clip from Khan Academy does a perfect job of
explaning this. Hope it helps.
|
|
|