you want to estimate p= the true proportion of students at your school who have their drivers license. Which of the following is the smallest number of students that should be surveyed to estimate p with a margin of error of no more than .05 with 90% confidence?
A. 300
B. 275
C. 250
D. 225
E. 200
I know the answer is B but I have no idea how to get to that answer.
Ive tried using the Margin of Error formula and solving for N but I'm 59.04 as an answer for N.
I'm coming up with a MINIMUM sample size of 270.603, which when rounded up, becomes: 271. The SAMPLE PROPORTION closest to this is 275 (CHOICE B).
The ESTIMATED SAMPLE PROPORTION was calculated using the following formula: 
Now, since NO PRELIMINARY ESTIMATE WAS GIVEN/WAS AVAILABLE, then .5(50%) should be used for p-hat, or for the ASSUMED proportion
With p-hat being .5, q-hat = 1 - p-hat = 1 - .5 = .5
Since this is a 90% CONFIDENCE INTERVAL, then significance level is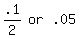 
, and so, 
E (Margin of Error) = .05
Therefore, becomes: 
In addition, when I used STATDISK to calculate the ESTIMATED SAMPLE PROPORTION, I got the same result: 271 students.
