Question 1058154: Sally Sethness assembles stereo equipment for resale in her shop. She offers two products, turntables and cassette players. She makes a profit of $10 on each turntable $6 on each cassette. Both must go through two steps in her shop - assembly and bench checking. A turntable take 12 hours to assemble and 4 hours to bench check. A cassette player take 4 hours assemble and 8 hours to bench check. Looking at this month's schedule, Sally sees that she has 60 assembly hours uncommitted and 40 hours of bench-checking time available. Find her best combinations of turntables and cassette player. What is the total profit on the combination you found?
Found 2 solutions by ewatrrr, ikleyn:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! 12t + 4c = 60 assemble
4t + 8c = 40 benchcheck
|Divide 2nd EQ by -2 to eliminate c
12t + 4c = 60
-2t - 4c = -20
10t = 40
t = 4 and c = 3
| 4($10) + 3($6) = $58
Answer by ikleyn(52937)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Sally Sethness assembles stereo equipment for resale in her shop.
She offers two products, turntables and cassette players.
She makes a profit of $10 on each turntable and $6 on each cassette.
Both must go through two steps in her shop—assembly and bench checking.
A turntable takes 12 hours to assemble and 4 hours to bench check.
A cassette player takes 4 hours to assemble but 8 hours to bench check.
Looking at this month's schedule, Sally sees that she has 60 assembly hours uncommitted
and 40 hours of bench-checking time available.
Use graphic linear programming to find her best combination of turntables and cassette players.
What is the total profit on the combination you found?
~~~~~~~~~~~~~~~~~~~~~
Let X be the number of turntable and Y be the number of cassette players.
We want maximize the profit function
P(X,Y) = 10X + 6Y
under the following restrictions
12X + 4Y <= 60 (assembly time)
4X + 8Y <= 40 (bench check time)
X >= 0, Y >= 0
The plot of the feasibility domain is shown in the Figure below.
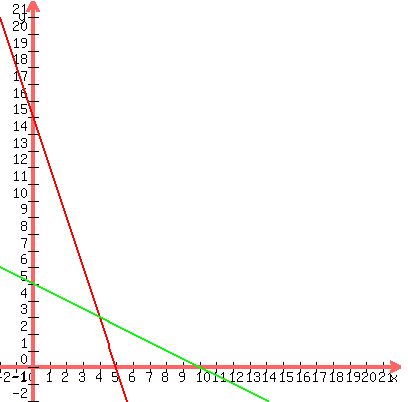 Plots y =
Plots y = 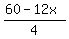 (red) and y = (red) and y = 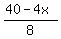 (green)
It is a quadrilateral in QI with the vertices at points P1 = (0,0), P2 = (0,5), P3 = (4,3), P4 = (5,0).
We apply the standard Linear Programming method in its geometric interpretation.
The solution is one of these 4 points, where the objective function (profit) has a maximum.
You calculate the values of the objective function P(X,Y) (profit) at listed points
P1: P(0,0) = 10*0 + 6*0 = 0,
P2: P(0,4) = 10*0 + 6*5 = 30,
P3: P(4,3) = 10*4 + 6*3 = 58,
P4: P(6,0) = 10*5 + 6*0 = 50.
Comparing these values, you find the optimal point.
It is P3: (X,Y) = (4,3), which means 4 turntables and 3 cassette players, providing maximum PROFIT of 58 dollars. (green)
It is a quadrilateral in QI with the vertices at points P1 = (0,0), P2 = (0,5), P3 = (4,3), P4 = (5,0).
We apply the standard Linear Programming method in its geometric interpretation.
The solution is one of these 4 points, where the objective function (profit) has a maximum.
You calculate the values of the objective function P(X,Y) (profit) at listed points
P1: P(0,0) = 10*0 + 6*0 = 0,
P2: P(0,4) = 10*0 + 6*5 = 30,
P3: P(4,3) = 10*4 + 6*3 = 58,
P4: P(6,0) = 10*5 + 6*0 = 50.
Comparing these values, you find the optimal point.
It is P3: (X,Y) = (4,3), which means 4 turntables and 3 cassette players, providing maximum PROFIT of 58 dollars.
Solved.
--------------
If you want to see many other similar and different solved problems, look into the lesson
- Solving minimax problems by the Linear Programming method
in this site.
|
|
|