SOLUTION: T =a+b e^-kt (Equation 2) where T is the temperature at time t, and a, b and k are constants with values a = 20 C, b = 80 C and k = 2.6 × 10^-4 ^-

Algebra ->  Probability-and-statistics -> SOLUTION: T =a+b e^-kt (Equation 2) where T is the temperature at time t, and a, b and k are constants with values a = 20 C, b = 80 C and k = 2.6 × 10^-4 ^-      Log On


   

Question 1033098: T =a+b e^-kt (Equation 2)
where T is the temperature at time t, and a, b and k are constants with
values a = 20 C, b = 80 C and k = 2.6 × 10^-4 ^-s1.
Differentiate Equation 2 with respect to t and thus give values (with
appropriate units and to two significant figures) for the rate of change of
temperature with time at times of 1.0 × 10^3 s and 5.0 × 10^3 s.


Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Your post displayed with strange character codes,
but maybe your equation was T=a%2Bb%2Ae%5E%28-kt%29 , with
a=20%5EoC , b=80%5EoC , and k=2.6%2A10%5E%28-4%29s%5E%28-1%29 .
In that case, differentiating with respect to t , we get
dT%2Fdt=-bk%2Ae%5E%28-kt%29 for the rate of change of temperature with time.
So for time t=1.0%2A10%5E%28-3%29s , we have
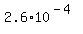k%2At=%22%28%222.6%2A10%5E%28-4%29s%5E%28-1%29%22%29%22%22%28%22t=1.0%2A10%5E%28-3%29s%22%29%22%22=+0.26%22 .
and that rate in degrees Celsius per second (rounded to 2 significant figures) would be
.
For time t=5.0%2A10%5E%28-3%29s , we have
k%2At=1.3 and the rate of temperature increase is

(in degrees Celsius per second, and rounded to 2 significant figures, of course).

NOTES:
Since the numerical values for a, b , k and t were all given with 2 significant figures, it makes sense to report results with 2 significant figures.
I was not sure that I could get the symbols for "degrees Celsius per second" to display properly, so I spelled it.