Question 1027094: The brand name of Domino's has a 75% recognition rate (each consumer is independent from each other). Assume 12 randomly selected consumers are surveyed. Use this situation to answer the questions below.
(a) Recognizing that this is a binomial situation, give the meaning/values of S, F, n, p, and q.
S is: n =
F is: p =
q =
(b) Construct the complete binomial probability distribution for this situation in a table at the right.
(c) Find the probability all twelve consumers recognize the Domino's brand.
(d) Find the probability less than five consumers recognize the Domino's brand.
(e) Find the mean and standard deviation of this binomial probability distribution.
(f) By writing a sentence, interpret the meaning of the mean found in (e).
(g) Would it be unusual for exactly six of the twelve consumers to recognize the Domino's brand? Explain your answer.
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website! The brand name of Domino's has a 75% recognition rate (each consumer is independent from each other). Assume 12 randomly selected consumers are surveyed. Use this situation to answer the questions below.
(a)Recognizing that this is a binomial situation, give the meaning/values of S, F, n, p, and q.
S is: n =
F is: p =
q =
(b)Construct the complete binomial probability distribution for this situation in a table at the right.
(c)Find the probability all twelve consumers recognize the Domino's brand.
(d)Find the probability less than five consumers recognize the Domino's brand.
(e)Find the mean and standard deviation of this binomial probability distribution.
(f)By writing a sentence, interpret the meaning of the mean found in (e).
(g)Would it be unusual for exactly six of the twelve consumers to recognize the Domino's brand? Explain your answer.
Solution:
(a) according to standard binomial distribution nomenclature,
n=sample size
p=probability of success
q=probability of failure, with condition that p+q=1, or q=1-p
S: event of success, in this case, brand is recognized.
F: event or failure, in this case, brand is not recognized.
(b) The binomial distribution, with variable x and above parameters, is given by
P(x;n;p)=
where C(n,x) is the binomial coefficient of choosing x object out of n, and where
C(n,x)=n!/(x!(n-x)!)
so the distribution is a table of x versus P(x;n;p) for x=0 to 12.
Here I will give you a kickstart:
Example, for x=9, n=12, p=0.75 (q=0.25), then
P(9,12,0.75)=
Proceeding to construct the table:
x P(x,12,0.75)
0 0.0000000596
1 0.0000021458
2 0.0000354052
3 0.0003540516
4 0.0023898422
5 0.0114712715
6 0.0401494503
... (please fill in the missing values as practice)
12 0.031676352
You can check your answers by adding up all (13) probabilities and they should add up to exactly one.
(c) If all consumers recognize the brand, that makes 12 successes, or x=12.
Consult table above to find probability.
(d) Less than 5 include the cases x=0,1,2,3,4. So you will need to sum the probabilities for x=0,1,2,3,4 accordingly.
(e) μ & σ
Mean of the binomial distribution is μ=np=12*0.75=9
standard deviation is given by σ=npq=12*0.75*0.25=2.25
(f) Mean of a distribution is the summation (discrete distribution) or integral (continuous distribution) of the value 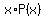 over the domain of the random variable. over the domain of the random variable.
In this case, μ=∑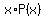 for x=0,1,2....12 for x=0,1,2....12
(g) From the table above, the probability that six of the 12 sampled will recognize the brand is P(6)=0.0401494503, or about 4%, or approximately 1 in 25 samples. Comment on whether this is an unusual occurrence.
|
|
|