Question 1019132: A class is taking a multiple-choice quiz that consists of 15 questions. Each question has 3 answer options: A, B, and C. The instructor made a mistake and printed the quiz for a much more advanced class. The students donít know any of the content and they randomly guess at every question.
Explain why this is a binomial random.
What are the values of the parameters n and p?
What is the mean quiz score?
What is the standard deviation of the quiz scores?
In order to pass, a student needs to get 9 or more questions correct. What is the probability that a student will get 9 or more questions correct?
What is the probability that a student will get exactly 9 questions correct?
What is the probability that a student will get all 15 questions correct?
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Question:
A class is taking a multiple-choice quiz that consists of 15 questions. Each question has 3 answer options: A, B, and C. The instructor made a mistake and printed the quiz for a much more advanced class. The students donít know any of the content and they randomly guess at every question.
a. Explain why this is a binomial random.
b. What are the values of the parameters n and p?
c. What is the mean quiz score?
d. What is the standard deviation of the quiz scores?
e. In order to pass, a student needs to get 9 or more questions correct.
What is the probability that a student will get 9 or more questions correct?
f. What is the probability that a student will get exactly 9 questions correct?
g. What is the probability that a student will get all 15 questions correct?
Solution:
a.
A situation must satisfy the following conditions in order that the binomial distribution be applicable.
1. The experiment must consist of a fixed and known number of trials, each of which must be random and independent of each other.
2. Each trial must be a Bernoulli trial, i.e. it must have exactly two outcomes, true or false, or success or failure.
3. The probability of success must be constant throughout the trials.
Since the given situation satisfies all of the requirements,
1. all answers are random guesses, and naturally, they are independent of each other. There are exactly 15 trials in the experiment.
2. answers to multiple choice questions must be either right or wrong, hence Bernoulli trial.
3. The probability of success is known (1/3) and is constant throughout the experiment (15 questions=15 trials).
The Binomial Distribution may be used to model the situation.
b.
parameters
n=number of trials = 15
p=probability of success in each trial = 1/3
c.
Mean, μ, of a binomial distribution = np = 15*(1/3) = 5
d.
variance, σ² = np(1-p) = 15*(1/3)(1-1/3) = 10/3
standard deviation, σ = √(10/3) = 1.826 approx.
e.
the probability of having X questions correct is given by the probability mass function (PMF)
P(X;n;p)=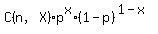
=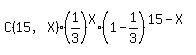
To get 9 or more questions correct, we can sum
Σ for i=9 to 15. for i=9 to 15.
= 0.02232+0.00670+0.00025+0.00003+0.00000+0.00000
=0.03083
f.
P(9;15;1/3)=0.02232 (from part (e))
g.
P(15;15,1/3)=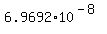
|
|
|