Question 1018955: A retail company must choose a few employees to send to a national retail conference. Of the 707 employees at this company, 504 are male. If 4 employees are randomly chosen, find the probability that exactly 3 are male.
Found 2 solutions by mathmate, robertb:
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Question:
A retail company must choose a few employees to send to a national retail conference. Of the 707 employees at this company, 504 are male. If 4 employees are randomly chosen, find the probability that exactly 3 are male.
Solution:
Choosing the first male is 504 out of 707.
Choosing the second male is 503 out of 706.
Choosing the third male is 502 out of 705.
The probability of randomly choosing male for all three is therefore the product of each, according to the multiplication rule.
P(3 males)
=(504*503*502)/(707*706*705)
=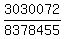
=0.362 (approximately)
Alternatively, if you have done hypergeometric distribution, it would be applicable here.
Let
A=number of males, 504
B=number of non-males, 707-504=203
a=number of males chosen, 3
b=number of non-males chosen, 0
and
C(n,r):=n!/(r!(n-r)!) [combination of r objects out of n]
P(a,b)=C(A,a)*C(B,b)/C(A+B,a+b)
=>
P(3,0)=C(504,3)*C(203,0)/C(707,3)
=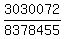 as before. as before.
The advantage of using hypergeometric distribution is that it is a systematic method, requiring very little input.
For example, the same problem but choosing 25 male candidates and 5 female candidates would be:
P(25,5)=C(504,25)*C(203,5)/C(707,30)
=0.057 (approximately)
Answer by robertb(5830)   (Show Source): (Show Source):
|
|
|