Question 1015438: Ren's chances of passing science is 0.35,
math 0.40 and both 0.12. Are the events
"Ren's passing science" and "Ren's passing math"
independent? What is the probability that she
fails both subjects?
Found 2 solutions by Theo, Edwin McCravy:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! if they were independent, then the probability of passing both science and math would be .35 * .40 = .14.
since it's .12, they are not independent events.
somehow one of them depends on the other in some way.
the probability that she fails both would be 1 minus the probability that she passes either science or math or both.
the probability that she passes one or the other or both would be .35 + .40 - .12 = .63
the probability that she doesn't pass either one would be 1 minus .63 = .37.
i believe that's right.
hopefully it agrees with what your solution should be.
if it's not, let me know what the solution should be and i'll try to figure out why it's not what i think it is.
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
His is correct solution. Here's a little more detail:
Let S be the event that she passes science.
Let M be the event that she passes math.
Ren's chances of passing science is 0.35, math 0.40 and both
0.12.
Are the events "Ren's passing science" and "Ren's passing
math" independent?
If so, then the conditional probability and the unconditional
probabilities would have to be the same:
     
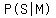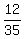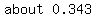They are not independent, because:
The probability of passing science, given no other
information, is 0.35, which is not the same as the probability
of her passing science, given that she passes math. which is a
little less, or about 0.343. This is probably due to the fact
that for her to pass math requires her to spend more time on
studying math and that would take away from her science study
time.
Or we could do it this way:
    
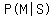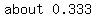They are not independent, because:
The probability of passing math, given no other information, is
0.40, which is not the same as the probability of her passing
math, given that she passes science. which is a little less, or
about 0.333. This is probably due to the fact that for her to
pass science requires her to spend more time on studying
science and that would take away from her math study time.
[Note: it was not necessary to do both, or even either one. We
could do it as the other tutor did and just multiply them and
see if P(S)*P(M)=P(S and M). I did it this long way to show
you that when you are given that one occurs, that changes the
probability of the other. That's the concept of the difference
between independent and independent events.]
What is the probability that she fails both subjects?
    
 
 
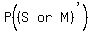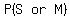
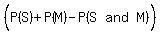
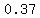Edwin
|
|
|
