Question 1007965: Can someone PLEASE HELP!!!
Suppose we want to determine the (binomial) probability (p) of getting 5 heads in 15 flips of a 2-sided coin. Using the Binomial table in the appendix of the text, what values of n, x, and p would we use to look up this probability, and what would be the probability?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! p(x) = c(n,x) * p^x * q^(n-x)
x = 5
n = 15
p = .5
q = .5
formula becomes:
p(5) = c(15,5) * .5^5 * .5^10
solve for p(5) to get:
p(5) = .0916442871
c(15,5) is the combination formula for the number of ways to select 5 things out of 15 where order doesn't matter.
the general formula is c(n,x) = n! / (x! * (n-x)!)
when n = 15 and x = 5, c(n,x) becomes:
c(15,5) = 15! / (5! * 10!) = (15*14*13*12*11*10!) / (5! * 10!)
this becomes:
c(15,5) = (15*14*13*12*11) / (5*4*3*2*1) which becomes (21*13*11 which is equal to 3003.
c(15,5) * p^x * q^(n-x) becomes 3003 * .5^5 * .5^10 which becomes 3003 * .5^15 which becomes .0916442871
that's the probability of getting exactly 5 heads out of 15 tosses.
the value of n is 15.
the value of x is 5
the value of p is .5
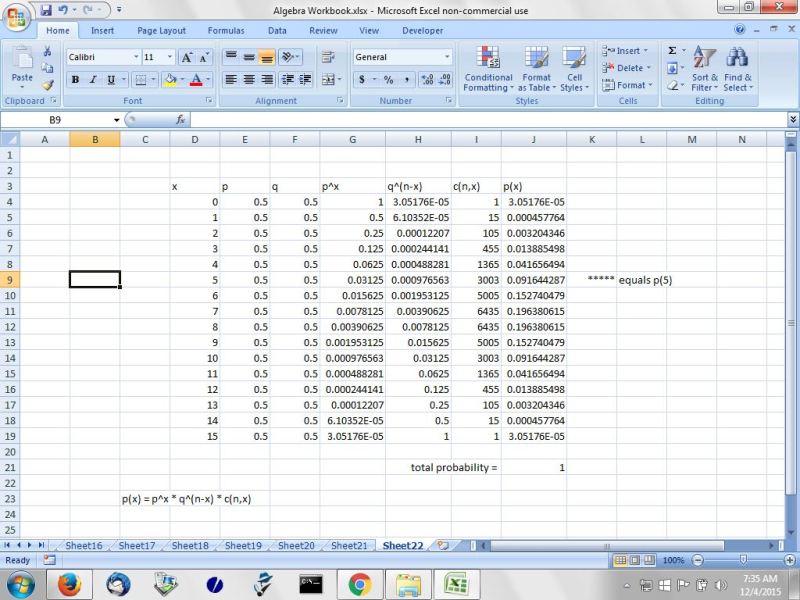
the full probability table for this problem is shown below:
the total probability is equal to 1 as it should be.
|
|
|