SOLUTION: I have 6 zeros, (x), (x-2), (x-5), (x-5), (x-7) and (x-9). How do I take these zeros and form them into a polynomial equation?

(x), (x-2), (x-5), (x-5), (x-7) and (x-9) 

are NOT zeros, they are FACTORS.

The zeros are 

0, 2, 5, 5, 7, and 9.  

Since 5 is listed twice it is said to
be a zero of multiplicity 2.

To find a polynomial with those zero, we start by setting 
x equal to each zero:

x=0, x=2, x=5, x=5, x=7, and x=9.  

Then we subtract the zero on the right from both sides of 
each of those 6 equations:

x-0=0, x-2=0, x-5=0, x-7=0, x-9=0

Then we use the principle that equals multiplied by equals gives
equals.

So we multiply all the left sides together and all the right sides
together.  (Multiplying all the right sides together just gives 0.)

(x-0)(x-2)(x-5)(x-5)(x-7)(x-9) = 0

And since x-0 is just x, we have

(x)(x-2)(x-5)(x-5)(x-7)(x-9) = 0

Those are the factors you gave.  But again, the zeros are
0,2,5,5,7,9

And after lots of multiplication we end up with:



Therefore the polynomial that has those 6 zeros is



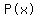I purposely left out the coefficient of  because some
teachers have complained that students have been just copying 
our answers and dishonestly turning them in for credit as though 
they had done the work themselves. 

Edwin