Question 959245: Having a lot of difficulty visualizing this don't know where to put the exponents could really use explanations:
The function f is a fifth-degree polynomial with
the x-intercepts -5, 2, and 10,
y-intercept 500 and
f (x) ≥ 0 for x ≤ 10.
Find f (x).
f (x) =
I don't understand what f(x)≥0 for x≤10 means, please explain that and how to solve for the rest.
Thank you
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
a fifth-degree polynomial with
the x-intercepts  , ,  , and , and  , ,
y-intercept  and and
 for for 
By hypothesis,  has factors has factors 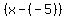 , , 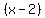 , and , and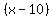 by the Factor Theorem. by the Factor Theorem.
==>  for some 2nd degree polynomial for some 2nd degree polynomial  . .
To determine  : :
We need  for for  . .
==>  for for 
Note that each factor is negative for some  . .
There a few ways to deal with this; here is one way.
Note that both 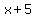 and and 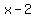 change signs when change signs when  , while , while  does not. does not.
Since we need  to be quadratic, we can take to be quadratic, we can take  for some constant for some constant  . .
Now, we have  for some for some  . .
Note: that we have not changed the x-intercepts by repeating some of the factors
Since 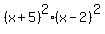 is never negative, needing is never negative, needing  for for  reduces to needing reduces to needing  for for  . .
*This is guaranteed if 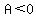 . .
Finally, we use  to determine to determine  : :




==> , which is indeed negative. , which is indeed negative.
Hence, we can take



|
|
|