Could you help me with this?
 =
=  Thank-you
Thank-you
 =
=  Add -1 to both sides to get the radical
term alone on the left:
Add -1 to both sides to get the radical
term alone on the left:
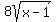 =
=  Square both sides of the equation:
Square both sides of the equation:
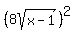 =
= 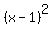
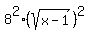 =
= 
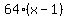 =
= 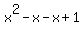
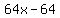 =
=  Switch left and right sides for convenience:
Switch left and right sides for convenience:
 =
= 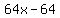 Get 0 on the right
Get 0 on the right
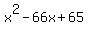 =
=  Factor left side by thinking of two whole numbers
which have product 65 and sum 66, whch are 65 and 1:
Factor left side by thinking of two whole numbers
which have product 65 and sum 66, whch are 65 and 1:
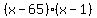 = 0
Set each factor = 0
= 0
Set each factor = 0
 gives
gives 
 gives
gives  However we must check these answers because radical
equations often have extraneous answers, which are
not solutions.
Checking
However we must check these answers because radical
equations often have extraneous answers, which are
not solutions.
Checking 
 =
= 
 =
= 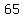
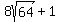 =
= 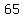
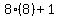 =
= 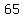
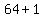 =
= 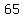
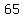 =
= 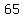 So we know
So we know  is a valid solution.
Checking
is a valid solution.
Checking 
 =
= 
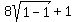 =
= 
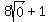 =
= 
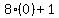 =
= 
 =
= 
 =
=  So as it turns out, both
So as it turns out, both  and
and  are valid solutions.
But be aware that this is not always the case.
Sometimes when you get two answers, one of them
will be a solution and the other will not check,
and thus must be discarded; sometimes neither one
is a solution and the equation has no solution.
Just be sure to ALWAYS CHECK a RADICAL EQUATION.
Edwin
are valid solutions.
But be aware that this is not always the case.
Sometimes when you get two answers, one of them
will be a solution and the other will not check,
and thus must be discarded; sometimes neither one
is a solution and the equation has no solution.
Just be sure to ALWAYS CHECK a RADICAL EQUATION.
Edwin