Question 906173: x to the fourth power - 20 x squared + 64 is greater than or equal to 0
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your problem is:
x^4 - 20x^2 + 64 >= 0
solve for x^4 - 20x^2 + 64 = 0 to find out when the graph crosses the x-axis.
this is a quadratic equation in disguise.
let y = x^2 and the equation becomes y^2 - 20y + 64 = 0
factor this equation to get (y-4)*(y-16)=0
solve for y to get y = 4 and y = 16
since y = x^2 and you want to solve for x, now replace y with x^2 to get:
x^2 = 4 and x^2 = 16
solve for x to get x = plus or minus 2 and x = plus or minus 4
if you did this correctly, your graph crosses the x-axis at x = -2, +2, -4, +4
since your original equation is x^2-20x+64 >= 0, then you need to test each interval of the graph to see where the graph is greater than 0 and less than 0.
since your zero points are -2, +2, -4, +4, then the intervals you need to test are:
x < -4
-4 < x < -2
-2 < x < 2
2 < x < 4
x > 4
you test by picking a point in each interval and testing if the graph is positive or negative at that point.
for example, at the point x = -3, the graph of x^4 - 20x^2 + 64 is equal to (-3)^4 - 20(-3)^2 + 64 = -35 which is negative.
this means that the graph is negative in the interval -4 < x < -2
you do that at all the other intervals and you'll get a picture of when the graph is above the x-axis and below the x-axis.
since the equation says that x^4 - 20x + 64 >= 0, then you pick the intervals that make that equation true.
as it turns out:
the intervals of x that satisfy the equation of x^2 - 20x + 64 >= 0 are:
x <= -4
-2 <= x <= 2
x >= 4
the graph of your equation is shown below:
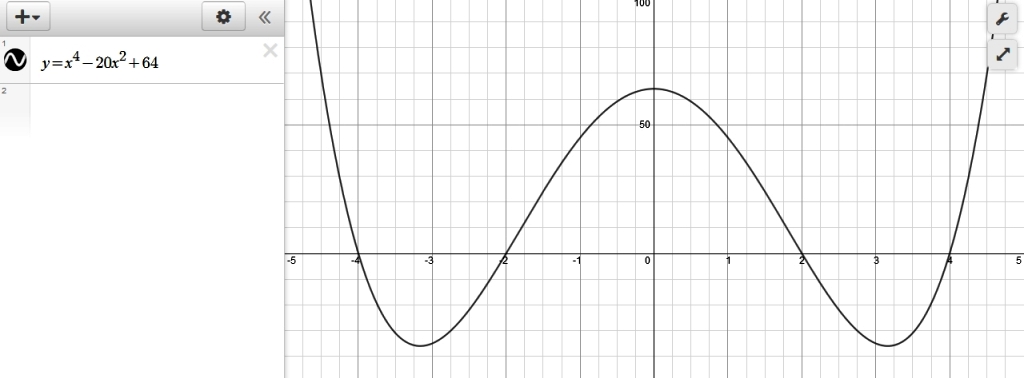
graphing is simpler, but if you didn't have graphing capability, then you needed to test each interval to find out if the equation was greater than or equal to 0 in that interval.
|
|
|