SOLUTION: Hello, Here is what I am currently working on and I am not sure if I am doing this right. Thank you for your help Given that either 2 or -2 is a solution to each of the follo

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Hello, Here is what I am currently working on and I am not sure if I am doing this right. Thank you for your help Given that either 2 or -2 is a solution to each of the follo      Log On


   

Question 88498: Hello,
Here is what I am currently working on and I am not sure if I am doing this right. Thank you for your help
Given that either 2 or -2 is a solution to each of the following, solve each equation
x^3-2x^2-6x+12=0

This is what I have done
2/1 -2 -6 -12
/- 2 0 0
-----------
1 0 0 0

2 is a solution -2 is not a solution
How do I solve the equation?
Thank you
Found 2 solutions by jim_thompson5910, stanbon:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Lets check the solution x=2 first

So let our test zero equal 2


Now set up the synthetic division table by placing the test zero in the upper left corner and placing the coefficients of the numerator to the right of the test zero.
2|1-2-612
|

Start by bringing down the leading coefficient (it is the coefficient with the highest exponent which is 1)
2|1-2-612
|
1

Multiply 2 by 1 and place the product (which is 2) right underneath the second coefficient (which is -2)
2|1-2-612
|2
1

Add 2 and -2 to get 0. Place the sum right underneath 2.
2|1-2-612
|2
10

Multiply 2 by 0 and place the product (which is 0) right underneath the third coefficient (which is -6)
2|1-2-612
|20
10

Add 0 and -6 to get -6. Place the sum right underneath 0.
2|1-2-612
|20
10-6

Multiply 2 by -6 and place the product (which is -12) right underneath the fourth coefficient (which is 12)
2|1-2-612
|20-12
10-6

Add -12 and 12 to get 0. Place the sum right underneath -12.
2|1-2-612
|20-12
10-60

Since the last column adds to zero, we have a remainder of zero. This means x=2 is a solution of x%5E3+-+2x%5E2+-+6x+%2B+12

Now lets look at the bottom row of coefficients:

The first 3 coefficients (1,0,-6) form the quotient

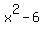
x%5E2+-+6


So %28x%5E3+-+2x%5E2+-+6x+%2B+12%29%2F%28x-2%29=x%5E2+-+6


So now lets solve 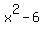x%5E2+-+6

x%5E2+-+6=0


Now let's use the quadratic formula to solve for x:


Starting with the general quadratic

ax%5E2%2Bbx%2Bc=0

the general solution using the quadratic equation is:

x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29

So lets solve x%5E2-6=0 (note: since the polynomial does not have an "x" term, the 2nd coefficient is zero. In other words, b=0. So that means the polynomial really looks like x%5E2%2B0%2Ax-6=0 notice a=1, b=0, and c=-6)

x+=+%28-0+%2B-+sqrt%28+%280%29%5E2-4%2A1%2A-6+%29%29%2F%282%2A1%29 Plug in a=1, b=0, and c=-6



x+=+%28-0+%2B-+sqrt%28+0-4%2A1%2A-6+%29%29%2F%282%2A1%29 Square 0 to get 0



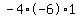x+=+%28-0+%2B-+sqrt%28+0%2B24+%29%29%2F%282%2A1%29 Multiply -4%2A-6%2A1 to get 24



x+=+%28-0+%2B-+sqrt%28+24+%29%29%2F%282%2A1%29 Combine like terms in the radicand (everything under the square root)



x+=+%28-0+%2B-+2%2Asqrt%286%29%29%2F%282%2A1%29 Simplify the square root



x+=+%28-0+%2B-+2%2Asqrt%286%29%29%2F2 Multiply 2 and 1 to get 2

So now the expression breaks down into two parts

x+=+%28-0+%2B+2%2Asqrt%286%29%29%2F2 or x+=+%28-0+-+2%2Asqrt%286%29%29%2F2


which simplifies to

x+=+sqrt%286%29 or x+=+-sqrt%286%29


So our solutions are:

x=2, x=sqrt%286%29 or x=-sqrt%286%29









------------------------------------------------------------------------------
Now lets see if x=-2 is a solution

So let our test zero equal -2

Now set up the synthetic division table by placing the test zero in the upper left corner and placing the coefficients of the numerator to the right of the test zero.
-2|1-2-612
|

Start by bringing down the leading coefficient (it is the coefficient with the highest exponent which is 1)
-2|1-2-612
|
1

Multiply -2 by 1 and place the product (which is -2) right underneath the second coefficient (which is -2)
-2|1-2-612
|-2
1

Add -2 and -2 to get -4. Place the sum right underneath -2.
-2|1-2-612
|-2
1-4

Multiply -2 by -4 and place the product (which is 8) right underneath the third coefficient (which is -6)
-2|1-2-612
|-28
1-4

Add 8 and -6 to get 2. Place the sum right underneath 8.
-2|1-2-612
|-28
1-42

Multiply -2 by 2 and place the product (which is -4) right underneath the fourth coefficient (which is 12)
-2|1-2-612
|-28-4
1-42

Add -4 and 12 to get 8. Place the sum right underneath -4.
-2|1-2-612
|-28-4
1-428

Since the last column adds to 8, we have a remainder of 8. This means x=-2 is not a solution of x%5E3+-+2x%5E2+-+6x+%2B+12
Since x=-2 is not a solution, this means that we cannot find any further roots

Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
Given that either 2 or -2 is a solution to each of the following, solve each equation
x^3-2x^2-6x+12=0

2/....1.... -2.... -6....+12
...............2......0.....-12
........1......0......-6..|..0
===============
Remainder is zero, so x=2 is a zero.
Quotient is x^2-6
Other zeroes are +sqrt6 and -sqrt6
============
Cheers,
Stan H.