Question 825866: Find all real solutions of the polynomial equation x^4-3x^3+6x-4=0 by using the Rational Zero Theorem and Synthetic division.
(The sollution to this problem is +1, +2, sqrt(2) and -(sqrt(2)) )
Possible rational zeros: +-1, +-2, +-4
So I did Synthetic division, and +1 worked out. But when I tried +2 with the quotient of the first division, the remainder was 4 which I hadn't expected because according to the answer sheet +2 is a zero.
Please help.
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! Both polynomial division and synthetic division require accounting for each variable placement value. The dividend should be  , in case you missed one of the terms.
I will give some results here, but because of slow task of writing on the site in text, my work is done separately on paper.
The first goal is find all of the rational roots. Later, the irrational ones are found using general solution to quadratic equation.
Test for possible roots, -1,-2,-4,1,2,4; for each you find, your unfound roots become much fewer.
(Synthetic Division used):
The check first for root of +1 gives remainder 0, resulting  ;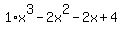
A check for root of +2 gives remainder 0, resulting  ;
This last expression is for the factor  , which has simply the solutions  and 
|
|
|
