Question 773385: Find all zeros of f(x) = x^3 - 7x^2 + 17x - 15 if 2 + i is one of the zeros of f(x).
(How does the zero product property play a role in solving this equation? I don't really understand how to use the zero product property in this sense).
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Is the function, f(x) factorable for complex numbers? What do you know about the zero product rule? Let a and b be complex numbers. If a*b=0 then either a=0 or b=0 or a=b=0. a or b being complex or real makes no difference.
In any case, rely on rational roots theorem to try to find .... wait! If you KNOW that 2+i is one of the zeros, then you KNOW 2-i is also a zero of f(x). You then have only one more zero to find.
Now, you can try Rational Roots Theorem if you wish to. You might try plusorminus 1, 3, 5, or 15. Only one of them will be a root. Best though to work with the two given and known complex roots, simplify their combined expression, and then do polynomial division on the dividend f(x).
Look at 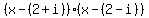 , multiply, simplify. That is one of the quadratic roots of f(x). This quadratic factor, ... is , multiply, simplify. That is one of the quadratic roots of f(x). This quadratic factor, ... is 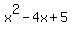 , after its simplifications. , after its simplifications.
------------------
THIS PART EDITED...
Trying Rational Roots Theorem and synthetic division, one REAL root is +3, so one factor of f(x) is (x-3).
The synthetic division testing for root of +3, gave the quotient 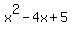 without any remainder. The roots of without any remainder. The roots of 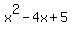 are in fact, are in fact, 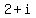 and and 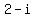 . Seeing that can be found through general solution to quadratic formula. . Seeing that can be found through general solution to quadratic formula.
FURTHER RECHECK:
In fact,  divided by divided by 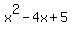 DOES give quotient of DOES give quotient of  without any remainder. Since without any remainder. Since 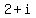 was given as one of the roots, this method would be the preferred method. was given as one of the roots, this method would be the preferred method.  is one of the factors of f(x). is one of the factors of f(x).
|
|
|