Horner's method is simply synthetic division.
x³ + 5x² + 8x + 6 = 0
The feasible rational roots are ± the factors of 6, which are
±1, ±2, ±3, ±6
It has no sign changes (all terms positive), so there are
no positive roots. So we need try only negative feasible
rational roots:
We try -1
-1|1 5 8 6
| -1 -4 -4
1 4 4 2
No, that doesn't give 0 on the far right.
We try -2
-2|1 5 8 6
| -2 -6 -4
1 3 2 2
No, that doesn't give 0 on the far right, either.
We try -3
-3|1 5 8 6
| -3 -6 -6
1 2 2 0
Whoopie do! That give 0 on the far right!
So we have have found one zero -3. The above
synthetic division is a shortcut for long division
of dividing by (x + 3) and getting x² + 2x + 2 as a
quotient, so we have now factored:
x³ + 5x² + 8x + 6 = 0
as
(x + 3)(x² + 2x + 2) = 0
Using the zero factor principle:
x + 3 = 0; x² + 2x + 2 = 0
x = -3 x = 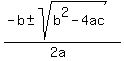 x =
x = 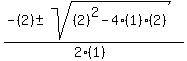 x =
x = 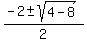 x =
x = 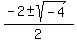 x =
x = 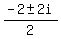 x =
x = 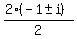 x =
x = 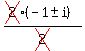 x = -1 ± i
So the three roots are -3, -1 + i, -1 - i
Edwin
x = -1 ± i
So the three roots are -3, -1 + i, -1 - i
Edwin