Question 75666: can i please get help with this?
x^2-10x+24=0
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
List the possible numbers that multiply to 24:
1,2,3,4,6,8,12,24
And you could also have negative numbers since (-8)(-3)=24. So of these possible factors, which 2 numbers add to -10? Lets look at (-8) and (-3), they multiply to 24 but add to -11, so that doesn't work. Lets look at (-12) and (-2): they add to -14, that doesn't work either. Finally lets look at (-6) and (-4): they add to -10 and that works. In practice this might take longer since I already knew the answer but just wanted to show the process. So the polynomial  factors to factors to
 which if foiled becomes which if foiled becomes  again. So now set each factor equal to zero individually. The reason why this works is because we can say again. So now set each factor equal to zero individually. The reason why this works is because we can say

 divide both sides by q divide both sides by q
and
 divide both sides by p. So if either p or q is 0 (or both) then the entire equation equals zero. divide both sides by p. So if either p or q is 0 (or both) then the entire equation equals zero.
The same applies to 
 divide both sides by (x-4) divide both sides by (x-4)

 Add 6 to both sides Add 6 to both sides

 divide both sides by (x-6) divide both sides by (x-6)

 Add 4 to both sides Add 4 to both sides

So the answers are x=6 or x=4
Or you could always plug the coefficients into the quadratic formula:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=4 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 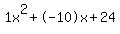 can be factored: can be factored:

Again, the answer is: 6, 4.
Here's your graph:
 |
|
|
|