Question 723112: How do you factor this completely? 6rcubed+15rsquared+8r+20
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The polynomial  would have a factor of the form would have a factor of the form 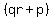
if 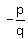 is a zero of the polynomial. is a zero of the polynomial.
Zeros of that polynomial must be negative because for all  , , and and 
Any rational zeros will be of the form 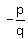 , ,
where  is a factor of the independent term, is a factor of the independent term,  , and , and
 is a factor of the leading coefficient is a factor of the leading coefficient  . .
So,  could be 1, 2, 3, or 6, and could be 1, 2, 3, or 6, and  could be 1, 2, 4, 5, 10, or 20. could be 1, 2, 4, 5, 10, or 20.



Since 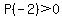 and and 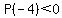 , there must be a zero of , there must be a zero of 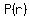 between -2 and -4. Of all the rational possibilities, only between -2 and -4. Of all the rational possibilities, only  and and 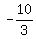 are between -2 and -4. are between -2 and -4.

so 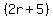 is a factor of is a factor of 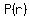 and dividing and dividing 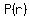 by by 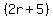 we get we get 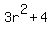 , which cannot be factored further, so , which cannot be factored further, so

NOTE: If you have gone beyond real numbers and are expected to use complex numbers, you could factor 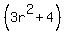 further. further.
|
|
|