Question 718805: Factorise 4x^3+10x^2+4x+3.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!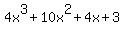 
The greatest common factor is 1 (which we rarely bother factoring out). With four terms this expression has too many terms for factoring by patterns or for trinomial factoring. And since I do not see how to factor this by grouping, we are left with factoring by trial and error of the possible rational roots.
Finding roots of a polynomial can help us find factors of the polynomial because if "r" is a root, then (x-r) is a factor. The possible rational roots of a polynomial are all the ratios/fractions, positive and negative, which can be formed using a factor of the constant term over a factor of the leading coefficient. The constant term, at the end, is 3. It's factors are 1 and 3. The leading coefficient, at the front, is 4. Its factors are 1, 2 and 4. This makes the possible rational roots:
+1/1, +3/1, +1/2, +3/2, +1/4 and +3/4
The first two will simplify:
+1, +3, +1/2, +3/2, +1/4 and +3/4
If you know Descartes' Rule of Signs and you notice that there are no sign changes in 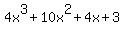, then you know that there are no positive roots. So now we are down to:
-1, -3, -1/2, -3/2, -1/4 and -3/4
Since powers of -1 are relatively easy we can check it mentally. -1 as a value for x does not make 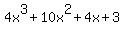zero so it is not a root. For the other possible roots, we're going to use synthetic division:
-3 | 4 10 4 3
----- -12 6 -30
----------------
4 -2 10 -27
The remainder is in the lower right corner. It is not zero so -3 is not a root and (x-(-3)) (or (x+3)) is not a factor.
-1/2 | 4 10 4 3
----- -2 -4 0
----------------
4 8 0 3
Not a root either. But this remainder is positive and the remainder for -3 was negative. This tells us there must be a root between -3 and -1/2. Unfortunately, none of the other possible rational roots work either. (Try them yourself if you don't believe me.) So this polynomial will not factor. (Are you sure you posted the right polynomial?)
FWIW: The graph of  is below. The x-coordinate of the point where it crosses the x-axis is the root we detected while checking the rational roots. It must be an irrational root.
|
|
|
