SOLUTION: What is the LMC of the pair of polynomials? 2x^2-18 and 5x^3+30x^2+45x=

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: What is the LMC of the pair of polynomials? 2x^2-18 and 5x^3+30x^2+45x=       Log On


   

Question 717184: What is the LMC of the pair of polynomials?
2x^2-18 and 5x^3+30x^2+45x=
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
To find the LCM of some polynomials you need to see their factors. So we will factor them. First the greatest common factor:
2x%5E2-18+=+2%28x%5E2-9%29
5x%5E3%2B30x%5E2%2B45x+=+5x%28x%5E2%2B6x%2B9%29
Next, factoring patterns. The second factor of the first polynomial is a difference of squares which will factor according to the pattern a%5E2-b%5E2+=+%28a%2Bb%29%28a-b%29. The second factor of the other polynomial fits a different pattern: a%5E2%2B2ab%2Bb%5E2+=+%28a%2Bb%29%5E2 or (a+b)(a+b) with the "a" being x and the "b" being 3. Using these patterns to further factor we get:
2x%5E2-18+=+2%28x%5E2-9%29+=+2%28x%2B3%29%28x-3%29
5x%5E3%2B30x%5E2%2B45x+=+5x%28x%2B3%29%5E2

If you have trouble with LCM's I find that it can be helpful to write the factors in a special way:
2x^2-18          = 1 * 2 * (x+3) * (x-3)
5x^3+30x^2+45x   = 1     * (x+3)         * 5 * x * (x+3)
========================================================
LCM              = 1 * 2 * (x+3) * (x-3) * 5 * x * (x+3) = 10x(x+3)(x-3)(x+3)
The first lines display the polynomials and their factors. The bottom line is the LCM. Notice how I used spacing and the Commutative Property (which allows me to rearrange the order of factors of the polynomials in any way I choose. I arranged the factors so the the factors in each column were all the same. I lined up the factors of 1, of 2, of (x+3), etc. Taking 1 factor from each column, the LCM is the product of these factors.

Sometimes you want an LCM in factored form (like when you are finding a lowest common denominator (LCD) which is just an LCM of denominators). Sometimes you want it in simplified form.

If you want this LCM in simplified form then we just multiply out the factors. We can multiply in any order so I am going to choose an order that looks easy. First, (x+3)(x-3). We already know how this works out from when we factored 2x^2=18:
LCM = 10x%28x%5E2-9%29%28x%2B3%29
Next I'll use FOIL to multiply the last two factors:
LCM = 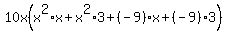10x%28x%5E2%2Ax%2Bx%5E2%2A3%2B%28-9%29%2Ax%2B%28-9%29%2A3%29
Simplifying...
LCM = 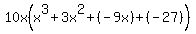10x%28x%5E3%2B3x%5E2%2B%28-9x%29%2B%28-27%29%29
And finally the 10x (with the Distributive Property):
LCM = 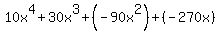10x%5E4%2B30x%5E3%2B%28-90x%5E2%29%2B%28-270x%29

P.S. There are additional uses for arranging the factors in a table like the one above:
  • This table will handle as many polynomials as you need. Just add a line for each additional polynomial.
  • If you are looking for an LCD, not only can you find the LCD but you can see what you need to multiply each fraction by to make the denominator become the LCD. For example, if the problem was to add:
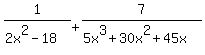
    1%2F%282x%5E2-18%29+%2B+7%2F%285x%5E3%2B30x%5E2%2B45x%29
    the LCD would be as was found earlier. And from the table you can literally see which factors of the LCD a certain denominator is missing. For 2x^2-18 we can see that it is "missing" factors of 5, x and a second (x+3). And for the other denominator we can see that, compared to the LCM/LCD, it is "missing" factors of 2 and (x-3). We now now how to change the fractions so their denominators become the LCD:
    etc.
  • This table of factors can also be used to find the greatest common factor (GCF) between polynomials. In this case, instead of using factors from every column you use only the factors from "full" columns. IOW from columns that have no empty spaces. In this case there are only two "full" columns: the 1's and the first (x+3)'s. So the GCF for 2x^2-18 and 5x^3+30x^2+45x is 1*(x+3) or just (x+3)