Question 709890: how do you solve x^4+x^2-30 ?
Answer by josh_jordan(263)   (Show Source): (Show Source):
You can put this solution on YOUR website! To solve, let's first factor our expression: x^4 + x^2 - 30. What two numbers, when multiplied, give us -30, and when added, give us 1? Let's find out:
-1 x 30 = -30; -1 + 30 = 29 NO
-2 x 15 = -30; -2 + 15 = 13 NO
-3 x 10 = -30; -3 + 10 = 7 NO
-5 x 6 = -30; -5 + 6 = 1 YES!!
Since -5 and 6 work, we will now factor our expression:
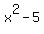
To find x, we will set each of these factors equal to 0:
x^2 - 5 = 0 =
Add 5 to both sides:
x^2 = 5
Finally, take the square root of both sides, remembering to add a +- sign. This gives us

Now, take our other factor and set to zero:
x^2 + 6 = 0
Subtract 6 from both sides, giving us
x^2 = -6
Take the square root of both sides, remembering to add a +- sign to the right side equation:

Remember that since  , , 
Our final answer is x =  , ,  , , 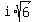 , and , and 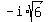
|
|
|