Question 696202: "Find the roots of the polynomial equation." 2x^3+2x^2-19x+20
I tried factoring out a 2 but it is uneven. Can I still find the roots and solve the problem even when the x^3 coefficient is two?
I need this right now ASAP because I have an Alg. 2 final tomorrow, thanks
Found 2 solutions by solver91311, KMST:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The rational roots of  (if they exist) will be of the form (if they exist) will be of the form
 and and 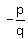 where where  is a factor of the independent term is a factor of the independent term  and and  is a factor of the leading coefficient is a factor of the leading coefficient  . .
Factors of  : :  , ,  , ,  , ,  , ,  , ,  . Factors of . Factors of  : :  , ,  . .
Possible rational roots:  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , and , and  . .
I tried them, and found that  , and that , and that
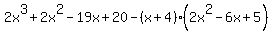
The roots would be  , ,
and the solutions to  . .
However,  has no real solution. has no real solution.
If you are studying complex numbers, you could find another two complex roots.
|
|
|