Question 661682: Form a polynomial function Zeros: -2, multiplicity 2;4, multiplicity 1; degree 3
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! One answer is
You could multiply the whole thing by any non-zero number to get another solution.
To have  for a zero with multiplicity  ,
a polynomial must have  as a factor times.
An example would be 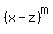 , but we can multiply that by any factor,
other than zero, and would still be a zero with multiplicity .
To get  as a zero, you need the factor
To get as a zero with multiplicicty  , you need to include as a factor
To get  as a zero, you need the factor
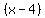
To have both,
as a zero with multiplicicty ,
and as a zero with multiplicicty  ,
you need to include  as a factor.
Since
is a polynomial of degree 3, you cannot include any other factors with the variable  ,
but you can multiply that polynomial by any real number other than zero,
and it will still be a polynomial of degree 3, with the required zeros.
|
|
|
