Question 639899: if f(x)= ax˛ + bx + c is divided by x+2, x-1, and x-3, it leaves a remainder of 64, 1, and 22, respectively.
find a + b + c?
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
if f(x)= ax˛ + bx + c is divided by x+2, x-1, and x-3, it leaves a remainder of 64, 1, and 22, respectively.
=========================================================================
The remainder theorem tells us that if we divide a polynomial f(x) by
x-a, the remainder will be f(a).
=========================================================================
Therefore:
The remainder theorem tells us that if we divide f(x) = ax˛ + bx + c by
x+2, the remainder will be f(-2), which is a(-2)˛+b(-2)+c or 4a-2b+c and
since that's given to be 64 we have the equation:
4a-2b+c = 64
The remainder theorem tells us that if we divide f(x) = ax˛ + bx + c by
x-1, the remainder will be f(1), which is a(1)˛+b(1)+c or a+b+c and
since that's given to be 1 we have the equation:
a+b+c = 1
The remainder theorem tells us that if we divide f(x) = ax˛ + bx + c by
x-3, the remainder will be f(3), which is a(3)˛+b(3)+c or 9a+3b+c and
since that's given to be 22 we have the equation:
9a+3b+c = 22
So we have the system of three equations:
4a-2b+c = 64
a+ b+c = 1
9a+3b+c = 22
Solve that system and get a=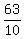 , b= , b=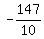 and c= and c=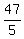 Those are terrible fractions, but they are correct.
Edwin
Those are terrible fractions, but they are correct.
Edwin
|
|
|